摘要： 我们把边长为1的等边三角形PQR沿着边长为整数的正n边形的边按照如图(1)的方式连续转动.当顶点P回到正n边形的内部时.我们把这种状态称为它的“点回归 ,当△PQR回到原来的位置时.我们把这种状态称它的“三角形回归 . 例如.如图(2)边长为1的等边三角形PQR的顶点P在边长为1的正方形ABCD内.顶点Q与点A重合.顶点R与点B重合.△PQR沿着正方形ABCD的边BC.CD.DA.AB.-.连续转动.当 △PQR连续转动3次时.顶点P回到正方形ABCD内部.第一次出现P的“点回归 , △PQR连续转动4次时△PQR回到原来的位置.出现第一次△PQR的“三角形回归 ． 操作: 如图(3).如果我们把边长为1的等边三角形PQR沿着边长为1的正五边形ABCDE的边连续转动.则连续转动的次数k= 时.第一次出现P的“点回归 ,连续转动的次数k= 时.第一次出现△PQR的“三角形回归 ． 猜想:我们把边长为1的等边三角形PQR沿着边长为1的正n边形的边连续转动． (1)连续转动的次数k= 时.第一次出现P的“点回归 , (2)连续转动的次数k= 时.第一次出现△PQR的“三角形回归 , (3)第一次同时出现P的 “点回归 与△PQR的“三角形回归 时.写出连续转动的次数k与正多边形的边数n之间的关系．
网址：http://m.1010jiajiao.com/timu3_id_8753[举报]
如图所示，已知等边△OAB的边长为a，以边AB上的高OA1为边，按逆时针方向作等边△OA1B1，A1B1与OB相交于点A2，若再以OA2为边按逆时针方向作等边△OA2B2，A2B2与OB1相交于点A3，按此作法进行下去，得到△OA3B3，△OA4B4，…，△OAnBn．
则△OA６B６的边长为 ．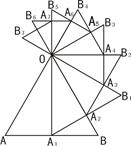
查看习题详情和答案>>
则△OA６B６的边长为 ．
查看习题详情和答案>>
23、（1）我们把直接从自然取得的能源称为一级能源，一级能源经过加工取得的能源称为二级能源．下列是目前正在利用和开发的部分能源 ①煤；②汽油；③天然气；④太阳能；⑤风能；⑥潮汐能；⑦地热能；⑧电能；⑨氢能；⑩酒精，其中不属于一级能源的是（填序号）
（2）我国是世界产煤大国．但含硫煤燃烧排放的SO2会引起“酸雨”现象．为减少大气污染，某发电厂采用了“石灰固硫法”，即向煤中掺入熟石灰，用来吸收SO2，写出“固硫法”反应的化学方程式
（3）科学家预言，氢能将成为21世纪的主要绿色能源，而水是自然界中广泛存在的物质，你认为获取氢气的最佳途径是
（4）电池是一种将
查看习题详情和答案>>
②⑧⑨⑩
．（2）我国是世界产煤大国．但含硫煤燃烧排放的SO2会引起“酸雨”现象．为减少大气污染，某发电厂采用了“石灰固硫法”，即向煤中掺入熟石灰，用来吸收SO2，写出“固硫法”反应的化学方程式
SO2+Ca（OH）2=CaSO3+H2O
．（3）科学家预言，氢能将成为21世纪的主要绿色能源，而水是自然界中广泛存在的物质，你认为获取氢气的最佳途径是
光分解海水
，氢能源的优点有无污染
、发热高、来源广、是再生能源等．（4）电池是一种将
化学
能转化为电能的装置．锂电池是一种新型的高能电池，其质量轻，电容量大，颇受手机、手提电脑等制造商的青睐．某种锂电池的总反应式为Li+MnO2=LiMnO2，其中化合价发生变化的元素是Li和Mn
．31、能源问题日益受到人们的关注．
（1）我们把直接从自然取得的能源称为一级能源，一级能源经过加工取得的能源称为二级能源．下列是目前正在利用或开发的部分能源，其中属于一级能源的是（填序号）
①酒精；②汽油；③天然气；④氢能；⑤电能；⑥地热能
（2）我国是世界产煤大国，但含硫煤燃烧排放的SO2会引起“酸雨”现象．为减少大气污染，某发电厂采用了“石灰固硫法”，即向煤中掺入熟石灰，用来吸收SO2．写出“固硫法”反应的化学方程式
（3）科学家预言，氢能将成为21世纪的主要绿色能源，氢能源的优点有
（4）电池是一种将
查看习题详情和答案>>
（1）我们把直接从自然取得的能源称为一级能源，一级能源经过加工取得的能源称为二级能源．下列是目前正在利用或开发的部分能源，其中属于一级能源的是（填序号）
③⑥
；①酒精；②汽油；③天然气；④氢能；⑤电能；⑥地热能
（2）我国是世界产煤大国，但含硫煤燃烧排放的SO2会引起“酸雨”现象．为减少大气污染，某发电厂采用了“石灰固硫法”，即向煤中掺入熟石灰，用来吸收SO2．写出“固硫法”反应的化学方程式
Ca（OH）2+SO2═CaSO3+H2O
；（3）科学家预言，氢能将成为21世纪的主要绿色能源，氢能源的优点有
无污染
、发热高、来源广等；（4）电池是一种将
化学
能转化为电能的装置．锂电池是一种新型的高能电池，其质量轻，电容量大，颇受手机、手提电脑等制造商的青睐．某种锂电池的总反应式为Li+MnO2=LiMnO2，其中化合价升高的元素是Li
．
（1）我们把直接从自然界取得的能源称为一次能源，一次能源经过加工取得的能源称为二次能源．下列是目前正在利用和开发的部分能源①煤；②汽油；③天然气；④太阳能；⑤风能；⑥潮汐能；⑦地热能；⑧电能；⑨氢能；⑩酒精，其中不属于一次能源的是（填序号） ．
（2）我国是世界产煤大国．但含硫煤燃烧排放的SO2会引起“酸雨”现象．为减少大气污染，某发电厂采用了“石灰固硫法”，即向煤中掺入生石灰CaO，用来吸收SO2，写出“固硫法”反应的化学方程式 ．
（3）科学家预言，氢能将成为21世纪的主要绿色能源，而水是自然界中广泛存在的物质，你认为获取氢气的最佳途径是 ，目前要实现这个途径最关键的问题是要研制出 ．
（4）目前我国许多城市已使用乙醇汽油．我市是著名的商品粮基地，但每年都有大量的过期粮食--陈化粮出现，人们用陈化粮来生产酒精，其过程为：陈化粮
葡萄糖
酒精+二氧化碳，试写出由葡萄糖制取的化学方程式 ．
（5）电池是一种将 能转化为电能的装置．锂电池是一种新型的高能电池，其质量轻，电容量大，颇受手机、手提电脑等制造商的青睐．某种锂电池的总反应式为Li+MnO2=LiMnO2，其中化合价发生变化的元素是 ．
查看习题详情和答案>>
（2）我国是世界产煤大国．但含硫煤燃烧排放的SO2会引起“酸雨”现象．为减少大气污染，某发电厂采用了“石灰固硫法”，即向煤中掺入生石灰CaO，用来吸收SO2，写出“固硫法”反应的化学方程式
（3）科学家预言，氢能将成为21世纪的主要绿色能源，而水是自然界中广泛存在的物质，你认为获取氢气的最佳途径是
（4）目前我国许多城市已使用乙醇汽油．我市是著名的商品粮基地，但每年都有大量的过期粮食--陈化粮出现，人们用陈化粮来生产酒精，其过程为：陈化粮
| 淀粉酶 |
| 酒化酶 |
（5）电池是一种将
（2012?门头沟区一模）能源问题日益受到人们的关注．
（1）我们把直接从自然界取得的能源称为一级能源，一级能源经过加工取得的能源称为二级能源．下列是目前正在利用或开发的部分能源，其中属于一级能源的是（填序号）
（2）我国是世界产煤大国，但含硫煤燃烧排放的SO2会引起“酸雨”现象．为减少大气污染，某发电厂采用了“石灰固硫法”，即向煤中掺入熟石灰，用来吸收SO2．SO2和熟石灰反应与CO2相似，写出“固硫法”反应的化学方程式
（3）科学家预言，氢能将成为21世纪的主要绿色能源，氢能源的优点有
查看习题详情和答案>>
（1）我们把直接从自然界取得的能源称为一级能源，一级能源经过加工取得的能源称为二级能源．下列是目前正在利用或开发的部分能源，其中属于一级能源的是（填序号）
③⑥
③⑥
；①酒精；②汽油；③天然气；④氢能；⑤电能；⑥地热能（2）我国是世界产煤大国，但含硫煤燃烧排放的SO2会引起“酸雨”现象．为减少大气污染，某发电厂采用了“石灰固硫法”，即向煤中掺入熟石灰，用来吸收SO2．SO2和熟石灰反应与CO2相似，写出“固硫法”反应的化学方程式
Ca（OH）2+SO2═CaSO3+H2O
Ca（OH）2+SO2═CaSO3+H2O
；（3）科学家预言，氢能将成为21世纪的主要绿色能源，氢能源的优点有
无污染
无污染
、发热高、来源广等．