摘要：1． 如图.设抛物线的焦点为F.动点P在直线上运动.过P作抛物线C的两条切线PA.PB.且与抛物线C分别相切于A.B两点. (1)求△APB的重心G的轨迹方程. (2)证明∠PFA=∠PFB. 解:(1)设切点A.B坐标分别为. ∴切线AP的方程为: 切线BP的方程为: 解得P点的坐标为: 所以△APB的重心G的坐标为 . 所以.由点P在直线l上运动.从而得到重心G的轨迹方程为: (2)方法1:因为 由于P点在抛物线外.则 ∴ 同理有 ∴∠AFP=∠PFB. 方法2:①当所以P点坐标为.则P点到直线AF的距离为: 即 所以P点到直线BF的距离为: 所以d1=d2.即得∠AFP=∠PFB. ②当时.直线AF的方程: 直线BF的方程: 所以P点到直线AF的距离为: .同理可得到P点到直线BF的距离.因此由d1=d2.可得到∠AFP=∠PFB.
网址：http://m.1010jiajiao.com/timu3_id_538527[举报]
22．如图，设抛物线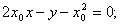
的焦点为F，动点P在直线
上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点.
的焦点为F，动点P在直线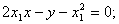上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点.（1）求△APB的重心G的轨迹方程.
（2）证明∠PFA=∠PFB.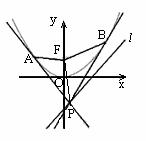
如图，设抛物线C:y=x2的焦点为F，动点P在直线l∶x-y-2=0上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点.
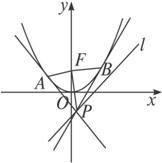
（1）求△APB的重心G的轨迹方程.
（2）证明∠PFA=∠PFB.
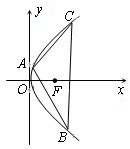
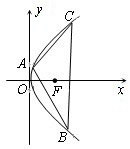
查看习题详情和答案>>如图，抛物线的顶点在坐标原点，且开口向右，点A，B，C在抛物线上，△ABC的重心F为抛物线的焦点，直线AB的方程为
。
（Ⅰ）求抛物线的方程；
（Ⅱ）设点M为某定点，过点M的动直线l与抛物线相交于P，Q两点，试推断是否存在定点M，使得以线段PQ为直径的圆经过坐标原点？若存在，求点M的坐标；若不存在，说明理由。
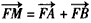，则点M在一定直线上，试证明之。
。
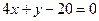