题目内容
如图,抛物线的顶点在坐标原点,且开口向右,点A,B,C在抛物线上,△ABC的重心F为抛物线的焦点,直线AB的方程为![]() 。
。
(Ⅰ)求抛物线的方程;
(Ⅱ)设点M为某定点,过点M的动直线l与抛物线相交于P,Q两点,试推断是否存在定点M,使得以线段PQ为直径的圆经过坐标原点?若存在,求点M的坐标;若不存在,说明理由。
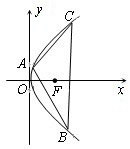
(Ⅰ)y2=16x
(Ⅱ)![]()
解析:
(Ⅰ)设抛物线方程为![]() ,
,
联立![]() 消去x,得
消去x,得![]() 。 (2分)
。 (2分)
设点![]() ,则
,则![]() ,
,
所以![]() 。 (4分)
。 (4分)
设点![]() ,因为△ABC的重心为
,因为△ABC的重心为![]() ,则
,则
![]() ,所以
,所以![]() 。 (5分)
。 (5分)
因为点C在抛物线上,则![]() ,解得p=8,此时
,解得p=8,此时![]() 。
。
故抛物线方程为y2=16x。 (6分)
(Ⅱ)设过定点M的动直线l的方程为![]()
![]() ,代入抛物线方程y2=16x,得
,代入抛物线方程y2=16x,得
![]() ,所以
,所以![]() 。 (8分)
。 (8分)
若以线段PQ为直径的圆经过坐标原点,则![]() ,即
,即![]() 。
。
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 。 (10分)
。 (10分)
所以直线l的方程为![]() ,即
,即![]() ,从而直线l必经过定点
,从而直线l必经过定点![]() 。(11分)
。(11分)
若直线l的斜率不存在,因为直线![]() 与抛物线的交点为
与抛物线的交点为![]() ,此时仍有
,此时仍有![]() 。故存在定点
。故存在定点![]() 满足条件。 (13分)
满足条件。 (13分)

练习册系列答案
相关题目
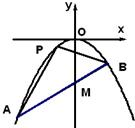 如图,抛物线的顶点O在坐标原点,焦点在y轴负半轴上.
如图,抛物线的顶点O在坐标原点,焦点在y轴负半轴上. 的顶点为坐标原点
的顶点为坐标原点 ,焦点
,焦点 在
在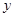 轴上,准线
轴上,准线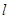 与圆
与圆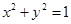 相切.
相切.
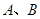 在抛物线
在抛物线 ,求点
,求点 的坐标.
的坐标.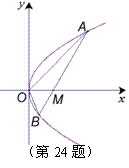 ①当
①当