摘要：3．直线与圆的位置关系:l :f1(x .y)＝0．圆C :f2(x .y)＝0消y 得F(x2)＝0. (1)直线与圆相交:F(x .y)＝0中D ＞0,或圆心到直线距离d ＜r . 直线与圆相交的相关问题:①弦长|AB|＝·|x1 -x2|＝·.或|AB|＝2,②弦中点坐标(.),③弦中点轨迹方程. (2)直线与圆相切:F(x)＝0中D ＝0.或d ＝r ．其相关问题是切线方程．如P(x0 .y0)是圆x2 +y2 ＝r2 上的点.过P 的切线方程为x0x +y0y ＝r2 .其二是圆外点P(x0 .y0)向圆到两条切线的切线长为或,其三是P(x0 .y0)为圆x2 +y2 ＝r2 外一点引两条切线.有两个切点A .B .过A .B 的直线方程为x0x +y0y ＝r2 . (3)直线与圆相离:F(x)＝0中D ＜0,或d ＜r ,主要是圆上的点到直线距离d 的最大值与最小值.设Q 为圆C :(x -a) 2 +(y -b) 2 ＝r2 上任一点.|PQ|max ＝|PC|+r ,|PQ|min ＝|PQ|-r .是利用图形的几何意义而不是列出距离的解析式求最值．
网址：http://m.1010jiajiao.com/timu3_id_537294[举报]
如图，设抛物线C1：y2=4mx（m＞0）的准线与x轴交于F1，焦点为F2；以F1、F2为焦点，离心率e=
的椭圆C2与抛物线C1在x轴上方的一个交点为P．
（1）当m=1时，求椭圆的方程及其右准线的方程；
（2）是否存在实数m，使得△PF1F2的边长是连续的自然数，若存在，求出这样的实数m；若不存在，请说明理由；
（3）在（1）的条件下，直线l经过椭圆C2的右焦点F2，与抛物线C1交于A1、A2，如果以线段A1A2为直径作圆，试判断点P与圆的位置关系，并说明理由．
查看习题详情和答案>>
的椭圆C2与抛物线C1在x轴上方的一个交点为P．（1）当m=1时，求椭圆的方程及其右准线的方程；
（2）是否存在实数m，使得△PF1F2的边长是连续的自然数，若存在，求出这样的实数m；若不存在，请说明理由；
（3）在（1）的条件下，直线l经过椭圆C2的右焦点F2，与抛物线C1交于A1、A2，如果以线段A1A2为直径作圆，试判断点P与圆的位置关系，并说明理由．
查看习题详情和答案>>
（2013•崇明县一模）如图，椭圆E：| x2 |
| a2 |
| y2 |
| b2 |
（1）求椭圆E的方程；
（2）设动直线l：y=kx+m与椭圆E有且只有一个公共点P，且与直线x=4相交于点Q．试探究：①以PQ为直径的圆与x轴的位置关系？
②在坐标平面内是否存在定点M，使得以PQ为直径的圆恒过点M？若存在，求出M的坐标；若不存在，说明理由．
如图，椭圆
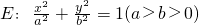的左焦点为F1，右焦点为F2，过F1的直线交椭圆于A，B两点，△ABF2的周长为8，且△AF1F2面积最大时，△AF1F2为正三角形．
的左焦点为F1，右焦点为F2，过F1的直线交椭圆于A，B两点，△ABF2的周长为8，且△AF1F2面积最大时，△AF1F2为正三角形．
的左焦点为F1，右焦点为F2，过F1的直线交椭圆于A，B两点，△ABF2的周长为8，且△AF1F2面积最大时，△AF1F2为正三角形．