题目内容
如图,椭圆 的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:①以PQ为直径的圆与x轴的位置关系?
②在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出M的坐标;若不存在,说明理由.

【答案】分析:(1)利用椭圆的定义、等边三角形的性质即可得出;
(2)①判断圆心到x轴的距离与半径的大小关系即可得出;
②假设平面内存在定点M满足条件,则由对称性知点M在x轴上,再利用直径所对的圆周角是直角即可求出.
解答:解:(1)∵△ABF2的周长为8,∴4a=8,∴a=2.
又当△AF1F2面积最大时为正三角形,∴A(0,b),a=2c,∴c=1,b2=3,
∴椭圆E的方程为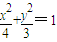
(2)①由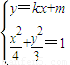 ,得方程(4k2+3)x2+8kmx+4m2-12=0
,得方程(4k2+3)x2+8kmx+4m2-12=0
由直线与椭圆相切得m≠0,△=0,⇒4k2-m2+3=0.
求得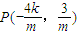 ,Q(4,4k+m),PQ中点到x轴距离
,Q(4,4k+m),PQ中点到x轴距离 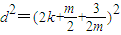
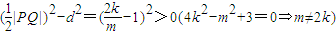 .
.
所以圆与x轴相交.
②假设平面内存在定点M满足条件,由对称性知点M在x轴上,设点M坐标为M(x1,0),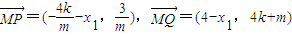 .
.
由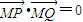 ,得
,得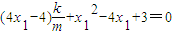 .
.
∴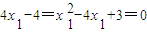 ,即x1=1.
,即x1=1.
所以定点为M(1,0).
点评:熟练掌握椭圆的定义、等边三角形的性质、直线与圆的位置关系的判断、圆的对称性、直径所对的圆周角是直角是解题的关键.
(2)①判断圆心到x轴的距离与半径的大小关系即可得出;
②假设平面内存在定点M满足条件,则由对称性知点M在x轴上,再利用直径所对的圆周角是直角即可求出.
解答:解:(1)∵△ABF2的周长为8,∴4a=8,∴a=2.
又当△AF1F2面积最大时为正三角形,∴A(0,b),a=2c,∴c=1,b2=3,
∴椭圆E的方程为
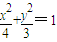
(2)①由
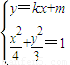 ,得方程(4k2+3)x2+8kmx+4m2-12=0
,得方程(4k2+3)x2+8kmx+4m2-12=0由直线与椭圆相切得m≠0,△=0,⇒4k2-m2+3=0.
求得
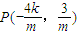 ,Q(4,4k+m),PQ中点到x轴距离
,Q(4,4k+m),PQ中点到x轴距离 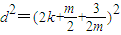
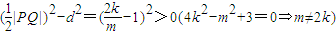 .
.所以圆与x轴相交.
②假设平面内存在定点M满足条件,由对称性知点M在x轴上,设点M坐标为M(x1,0),
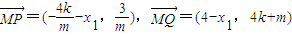 .
.由
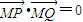 ,得
,得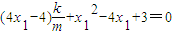 .
.∴
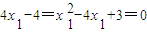 ,即x1=1.
,即x1=1.所以定点为M(1,0).
点评:熟练掌握椭圆的定义、等边三角形的性质、直线与圆的位置关系的判断、圆的对称性、直径所对的圆周角是直角是解题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
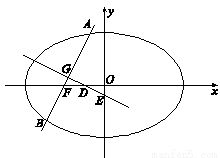
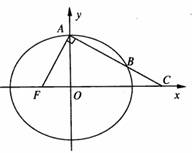 如图,椭圆
如图,椭圆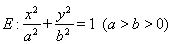
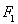
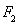
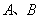
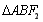
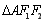
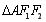

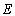
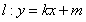
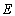
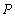
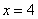
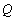
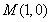
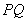
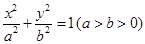 的左焦点为
的左焦点为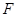 ,过点
,过点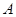 ,
,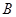 两点.当直线
两点.当直线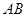 经过椭圆的一个顶点时,其倾斜角恰为
经过椭圆的一个顶点时,其倾斜角恰为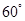 .
.
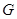 ,
,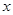 轴和
轴和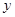 轴分别交于
轴分别交于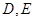 两点,
两点,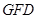 的面积为
的面积为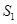 ,△
,△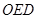 (
(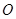 为原点)的面积为
为原点)的面积为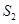 ,求
,求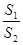 的取值范围.
的取值范围.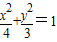 的左焦点为F,上顶点为A,过点A作直线AF的垂线分别交椭圆、x轴于B,C两点.
的左焦点为F,上顶点为A,过点A作直线AF的垂线分别交椭圆、x轴于B,C两点.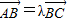 ,求实数λ的值;
,求实数λ的值;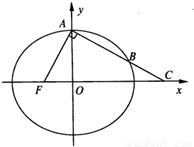
 的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.