摘要:1.关于直线对称问题: (1)关于l :Ax +By +C =0对称问题:不论点.直线与曲线关于l 对称问题总可以转化为点关于l 对称问题.因为对称是由平分与垂直两部分组成.如求P(x0 .y0)关于l :Ax +By +C =0对称点Q(x1 .y1).有=-(1)与A·+B·+C =0. (2)解出x1 与y1 ,若求C1 :曲线f(x .y)=0关于l :Ax +By +C1 =0对称的曲线C2 .由上面的中求出x0 =g1(x1 .y1)与y0 =g2(x1 .y1).然后代入C1 :f [g1(x1 .y1).g2(x2 .y2)]=0.就得到关于l 对称的曲线C2 方程:f [g1(x .y).g2(x .y)]=0. (3)若l :Ax +By +C =0中的x .y 项系数|A|=1.|B |=1.就可以用直接代入解之.尤其是选择填空题.如曲线C1 :y2 =4 x -2关于l :x -y -4=0对称的曲线l2 的方程为:(x -4) 2 =4(y +4)-2.即y 用x -4代.x 用y +4代.这样就比较简单了 (4)解有关入射光线与反射光线问题就可以用对称问题来解决 点与圆位置关系:P(x0 .y0)和圆C :(x -a) 2 +(y -b) 2 =r2. ①点P 在圆C 外有(x0 -a) 2 +(y0 -b) 2 >r2, ②点P 在圆上:(x0 -a) 2 +(y0 -b) 2 =r2, ③点P 在圆内:(x0 -a) 2 +(y0 -b) 2 <r2 .
网址:http://m.1010jiajiao.com/timu3_id_537293[举报]
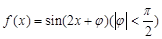 的图象向左平移
的图象向左平移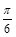 个单位后,所得图象关于原点对称,那么函数
个单位后,所得图象关于原点对称,那么函数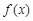 的图象 ( ).
的图象 ( ). 对称 B.关于直线
对称 B.关于直线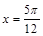 对称
对称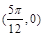 对称 D.关于直线
对称 D.关于直线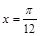 对称
对称 的最小正周期为π,若其图象向左平移
的最小正周期为π,若其图象向左平移 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( ) 对称
对称 对称
对称 对称
对称 对称
对称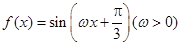 的最小正周期为
的最小正周期为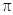 ,则函数
,则函数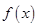 的图象( )
的图象( )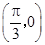 对称
对称 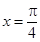 对称
对称 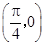 对称
对称 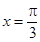 对称
对称  (其中
(其中 ),则函数
),则函数 的图象( ).
的图象( ). 对称 B.关于
对称 B.关于 轴对称
轴对称 轴对称 D.关于原点对称
轴对称 D.关于原点对称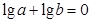 (其中
(其中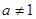 且
且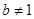 ),则函数
),则函数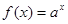 与
与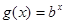 的图象( )
的图象( )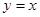 对称; B.关于
对称; B.关于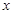 轴对称;
轴对称;
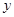 轴对称;
D.关于原点对称;
轴对称;
D.关于原点对称;