摘要:2.通过实例.了解两个互斥事件的概率加法公式,
网址:http://m.1010jiajiao.com/timu3_id_536848[举报]
下列说法正确的有( )
A.在独立性检验中,K2的值越大,两个分类变量之间的关系越强
B.回归分析是先通过直观图直观地了解两个变量的关系,然后通过最小二乘法建立回归模型,并通过分析相关指数、残差等评价模型的好坏
C.在对类似的问题作出推断时,我们不能仅凭主观意愿得出结论,而应通过试验收集数据,并依据假设检验的原理作出合理的推断
D.以上说法均正确
查看习题详情和答案>>甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:
甲校
乙校
(Ⅰ)计算x,y的值.
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
(Ⅲ)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
附:K2=
;
查看习题详情和答案>>
甲校
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频道 | 2 | 10 | 15 | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频道 | 1 | 2 | 9 | 8 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 10 | 10 | y | 3 |
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
附:K2=
| nad-bc2 |
| a+bc+da+cb+d |
| P(k2>k0) | 0.10 | 0.025 | 0.010 |
| K | 2.706 | 5.024 | 6.635 |
(2012•开封二模)甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样的方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下,规定考试成绩[120,150]内为优秀,
甲校:
乙校:
(1)计算x,y的值;
(2)由以上统计数据填写右面2×2列联表,若按是否优秀来判断,是否有97.5%的把握认为两个学校的数学成绩有差异.
(3)根据抽样结果分别估计甲校和乙校的优秀率;若把频率作为概率,现从乙校学生中任取3人,求优秀学生人数ξ的分布列和数学期望.
附:k2=
查看习题详情和答案>>
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 3 | 10 | 15 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | 10 | y | 3 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 9 | 8 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
(2)由以上统计数据填写右面2×2列联表,若按是否优秀来判断,是否有97.5%的把握认为两个学校的数学成绩有差异.
(3)根据抽样结果分别估计甲校和乙校的优秀率;若把频率作为概率,现从乙校学生中任取3人,求优秀学生人数ξ的分布列和数学期望.
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2>K) | 0.10 | 0.025 | 0.010 |
| K2 | 2.706 | 5.024 | 6.635 |
(2012•惠州一模)甲乙两个学校高三年级分别有1200人,1000人,为了了解两个学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两个学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
乙校:
(Ⅰ)计算x,y的值.
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率.
(Ⅲ)由以上统计数据填写右面2×2列联表,并判断是否有90%的把握认为两个学校的数学成绩有差异.
参考数据与公式:
由列联表中数据计算K2=
临界值表
查看习题详情和答案>>
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
(Ⅲ)由以上统计数据填写右面2×2列联表,并判断是否有90%的把握认为两个学校的数学成绩有差异.
参考数据与公式:
由列联表中数据计算K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
临界值表
| P(K≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
(本小题满分12分)甲乙两个学校高三年级分别有1200人,1000人,为了了解两个学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两个学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
|
分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
|
频数 |
3 |
4 |
8 |
15 |
|
分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
|
频数 |
15 |
x |
3 |
2 |
甲校:
|
分组 |
[70,80) |
[80,90) |
[90,100) |
[100,110) |
|
频数 |
1 |
2 |
8 |
9 |
|
分组 |
[110,120) |
[120,130) |
[130,140) |
[140,150] |
|
频数 |
10 |
10 |
y |
3 |
乙校:
(Ⅰ)计算x,y的值。
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率。
|
|
甲校 |
乙校 |
总计 |
|
优秀 |
|
|
|
|
非优秀 |
|
|
|
|
总计 |
|
|
|
(Ⅲ)由以上统计数据填写右面2×2列联表,并判断是否有90%的把握认为两个学校的数学成绩有差异。
参考数据与公式:
由列联表中数据计算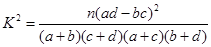
临界值表

查看习题详情和答案>>