题目内容
(2009全国卷Ⅰ文)(本小题满分12分)(注决:在试题卷上作答无效)
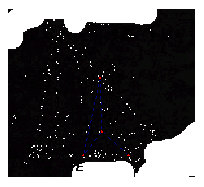
如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,点
,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 。
。
(I)证明:![]() 是侧棱
是侧棱![]() 的中点;
的中点;

![]() 求二面角
求二面角![]() 的大小。(同理18)
的大小。(同理18)
【解析】本小题考查空间里的线线关系、二面角,综合题。
(I)解法一:作![]() ∥
∥![]() 交
交![]() 于N,作
于N,作![]() 交
交![]() 于E,
于E,
连ME、NB,则![]() 面
面![]() ,
,![]() ,
,![]()
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]()
![]()
![]() 。
。
在![]() 中由
中由![]()
![]()
解得![]() ,从而
,从而![]()
![]() M为侧棱
M为侧棱![]() 的中点M.
的中点M.
解法二:过![]() 作
作![]() 的平行线.
的平行线.

(II)分析一:利用三垂线定理求解。在新教材中弱化了三垂线定理。这两年高考中求二面角也基本上不用三垂线定理的方法求作二面角。
过![]() 作
作![]() ∥
∥![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,作
,作![]() 交
交![]() 于
于![]() ,则
,则![]() ∥
∥![]() ,
,![]() 面
面![]() ,面
,面![]()
![]() 面
面![]() ,
,![]() 面
面![]()
![]()
![]() 即为所求二面角的补角.
即为所求二面角的补角.
法二:利用二面角的定义。在等边三角形![]() 中过点
中过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则点
,则点![]() 为AM的中点,取SA的中点G,连GF,易证
为AM的中点,取SA的中点G,连GF,易证![]() ,则
,则![]() 即为所求二面角.
即为所求二面角.
解法二、分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D—xyz,则![]() 。
。


(Ⅰ)设![]() ,则
,则
![]() ,
,
![]() ,由题得
,由题得
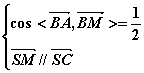 ,即
,即
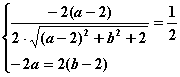 解之个方程组得
解之个方程组得![]() 即
即![]()
所以![]() 是侧棱
是侧棱![]() 的中点。
的中点。
法2:设![]() ,则
,则![]()
又![]()
故![]() ,即
,即
![]() ,解得
,解得![]() ,
,
所以![]() 是侧棱
是侧棱![]() 的中点。
的中点。
(Ⅱ)由(Ⅰ)得![]() ,又
,又![]() ,
,![]() ,
,
设![]() 分别是平面
分别是平面![]() 、
、![]() 的法向量,则
的法向量,则
 且
且 ,即
,即 且
且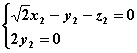
分别令![]() 得
得![]() ,即
,即
![]() ,
,
∴![]()
二面角![]() 的大小
的大小![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目