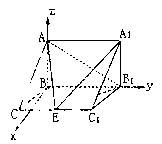
摘要:6.如图.在三棱柱中.侧面.为棱上异于的一点..已知.求: (Ⅰ)异面直线与的距离, (Ⅱ)二面角的平面角的正切值. 解:(I)以为原点..分别为轴建立空间直角坐标系. 由于. 在三棱柱中有 , 设 又侧面.故. 因此是异面直线的公垂线. 则.故异面直线的距离为. (II)由已知有故二面角的平面角的大小为向量的夹角.
网址:http://m.1010jiajiao.com/timu3_id_535854[举报]
如图,在三棱柱 中,
中, 侧面
侧面 ,
, 为棱
为棱 上异于
上异于 的一点,
的一点, ,已知
,已知 ,求:
,求:
(Ⅰ)异面直线 与
与 的距离;
的距离;
(Ⅱ)二面角 的平面角的正切值.
的平面角的正切值.
【解析】第一问中,利用建立空间直角坐标系
解:(I)以B为原点, 、
、 分别为Y,Z轴建立空间直角坐标系.由于,
分别为Y,Z轴建立空间直角坐标系.由于,

在三棱柱 中有
中有
 ,
,
设


又 侧面
侧面 ,故
,故 . 因此
. 因此 是异面直线
是异面直线 的公垂线,则
的公垂线,则 ,故异面直线
,故异面直线 的距离为1.
的距离为1.
(II)由已知有 故二面角
故二面角 的平面角
的平面角 的大小为向量
的大小为向量 与
与 的夹角.
的夹角.

查看习题详情和答案>>
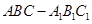 中,
中,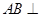 侧面
侧面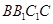 ,
,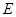 为棱
为棱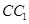 上异于
上异于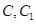 的一点,
的一点,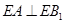 ,已知
,已知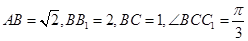 ,求:
,求: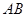 与
与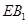 的距离;
的距离;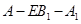 的平面角的正切值.
的平面角的正切值.
 如图,在三棱柱中,已知AB⊥侧面BB1C1C,
如图,在三棱柱中,已知AB⊥侧面BB1C1C,