摘要：(18')⑴证明命题: 若直线l过抛物线y2=2px ,交抛物线于AB两点,O为坐标原点, 那么·=-p2 ⑵写出第⑴题中命题的逆命题.如其为真,则给出证明; 如其为假,则说明理由 ⑶把第⑴题中命题作推广,使其是你推广的特例,并对你的推广作出证明
网址：http://m.1010jiajiao.com/timu3_id_534409[举报]
已知抛物线C：y2＝2px(p＞0)，直线l交C于E、F两点．
(1)求证：命题“若直线l过点A(2p，0)，则∠EOF＝90°(O为坐标原点)”是真命题；
(2)写出(1)中命题的逆命题，判断它是真命题还是假命题，并说明理由；
(3)将点A(2p，0)向右或向左移动为点A(c，0)，直线l过点A交C于E、F两点．当c＞2p及0＜c＜2p时，分别猜测∠EOF大小的变化情况(只须写出结论，不必证明)．
（2009•虹口区二模）（1）证明命题：若直线l过抛物线y2=2px （p＞0）的焦点F（
，0），交抛物线于AB两点，O为坐标原点，那么
•
=-
p2；
（2）写出第（1）题中命题的逆命题．如其为真，则给出证明； 如其为假，则说明理由；
（3）把第（1）题中命题作推广，使其是你推广的特例，并对你的推广作出证明．
查看习题详情和答案>>
| p |
| 2 |
| OA |
| OB |
| 3 |
| 4 |
（2）写出第（1）题中命题的逆命题．如其为真，则给出证明； 如其为假，则说明理由；
（3）把第（1）题中命题作推广，使其是你推广的特例，并对你的推广作出证明．
（1）证明命题：若直线l过抛物线y2=2px （p＞0）的焦点F（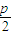
，0），交抛物线于AB两点，O为坐标原点，那么
•
=-
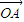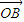p2；
（2）写出第（1）题中命题的逆命题．如其为真，则给出证明； 如其为假，则说明理由；
（3）把第（1）题中命题作推广，使其是你推广的特例，并对你的推广作出证明．
查看习题详情和答案>>
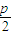，0），交抛物线于AB两点，O为坐标原点，那么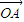•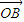=-p2；（2）写出第（1）题中命题的逆命题．如其为真，则给出证明； 如其为假，则说明理由；
（3）把第（1）题中命题作推广，使其是你推广的特例，并对你的推广作出证明．
查看习题详情和答案>>