摘要:(12')直三棱柱ABC-A1B1C1中的底面是等腰直角△,AB=AC=2,∠BAC=90°,棱AA1=3,若D是BC中点 理⑴求证:AD⊥平面BCC1B1) ⑵求异面直线DC1与AB1所成角的大小
网址:http://m.1010jiajiao.com/timu3_id_534406[举报]
(本小题满分12分)
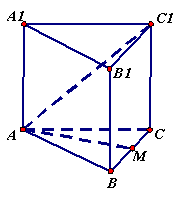 如图,正三棱柱ABC—A1B1C1的底面边长为a,点M在边 BC上,△AMC1是以点M为直角顶点的等腰直角三角形。
如图,正三棱柱ABC—A1B1C1的底面边长为a,点M在边 BC上,△AMC1是以点M为直角顶点的等腰直角三角形。
(Ⅰ)求证点M为边BC的中点;
(Ⅱ)求点C到平面AMC1的距离;
(Ⅲ)求二面角M—AC1—C的大小。
查看习题详情和答案>>
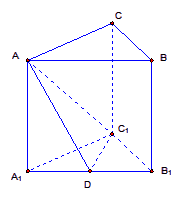
(12分)如图,直三棱柱ABC—A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=![]() ,D是线段A1B1??的中点.
,D是线段A1B1??的中点.
(1)证明:面![]() ⊥平面A1B1BA;
⊥平面A1B1BA;
(2)证明:![]() ;
;
(3)求棱柱ABC—A1B1C1被平面![]() 分成两部分的体积比.
分成两部分的体积比.
(12分)如图,直三棱柱ABC—A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=
 ,D是线段A1B1的中点.
,D是线段A1B1的中点. 
(1)证明:面
 ⊥平面A1B1BA;
⊥平面A1B1BA;(2)证明:
 ;
;(3)求棱柱ABC—A1B1C1被平面
 分成两部分的体积比.
分成两部分的体积比. ABC—A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=
ABC—A1B1C1的底面是等腰直角三角形,∠A1C1B1=90°,A1C1=1,AA1=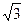 ,D是线段A1B1的中点.
,D是线段A1B1的中点. 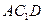 ⊥平面A1B1BA;
⊥平面A1B1BA;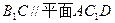 ;
; (本小题满分12分)如图,已知直三棱柱ABC—A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. (Ⅰ)求异面直线AB和C1D所成的角(用反三角函数表示);(Ⅱ)若E为AB上一点,试确定点E在AB上的位置,使得A1E⊥C1D;
(本小题满分12分)如图,已知直三棱柱ABC—A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. (Ⅰ)求异面直线AB和C1D所成的角(用反三角函数表示);(Ⅱ)若E为AB上一点,试确定点E在AB上的位置,使得A1E⊥C1D;