摘要:18. (1)证明:连结交于O.连结OD. 在中.点O和D都是中点 ∴OD||.又 ∴ 解:(2)∵BC.AC.两两垂直 ∴以C为原点建立空间直角坐标系 ∵..∴ ∴.... ∴.. 设为平面的法向量.则 .即 取.得..即解得 设点A到平面的距离为.则 ∴点A到平面的距离为. (3)设二面角的二面角为.则为锐角 又由(2)知为平面的法向量 ∴ ∴二面角的余弦值为 另解:设点P点AC中点.H为中点.连结DP.PH.DH ∴PD||BC.又 ∴.又 ∴ ∴为二面角的平面角.且 ∵. ∴.∴ ∴二面角的余弦值为
网址:http://m.1010jiajiao.com/timu3_id_534202[举报]
(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
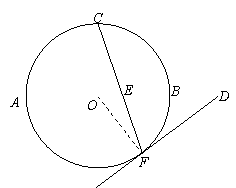 A. 选修4-1:几何证明选讲
A. 选修4-1:几何证明选讲
如图, 是⊙
是⊙ 的直径,
的直径,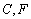 是⊙
是⊙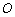 上的两点,
上的两点,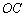 ⊥
⊥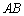 ,
,
过点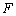 作⊙
作⊙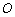 的切线FD交
的切线FD交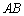 的延长线于点
的延长线于点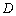 .连结
.连结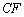 交
交
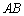 于点
于点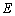 .
.
求证: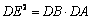 .
.
B. 选修4-2:矩阵与变换
求矩阵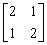 的特征值及对应的特征向量.
的特征值及对应的特征向量.
C. 选修4-4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是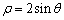 ,直线
,直线 的参数方程是
的参数方程是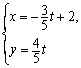 (
(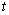 为参数).
为参数).
(1)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)设直线 与
与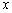 轴的交点是
轴的交点是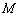 ,
,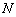 是曲线
是曲线 上一动点,求
上一动点,求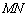 的最大值.
的最大值.
D.选修4-5:不等式选讲
设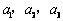 均为正数,且
均为正数,且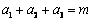 ,求证
,求证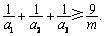
查看习题详情和答案>>
 如图,
如图, (II)设O为AC中点,若
(II)设O为AC中点,若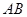 与
与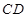 是
是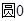 的直径,
的直径,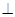
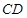 ,
,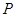 是
是 交
交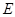 ,连
,连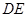 交
交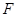 ,若
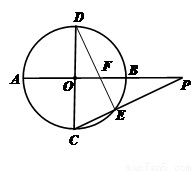
,若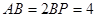 ,则
,则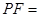 .
.
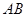 与
与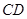 是
是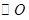 的直径,
的直径,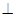
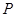 是
是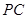 交
交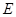 ,连
,连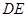 交
交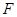 ,若
,若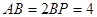 ,则
,则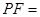 .
.