题目内容
(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
 A. 选修4-1:几何证明选讲
A. 选修4-1:几何证明选讲
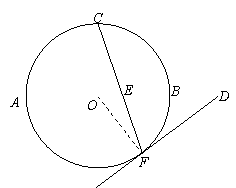
如图,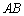 是⊙
是⊙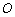 的直径,
的直径,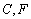 是⊙
是⊙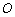 上的两点,
上的两点,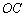 ⊥
⊥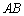 ,
,
过点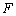 作⊙
作⊙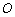 的切线FD交
的切线FD交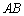 的延长线于点
的延长线于点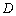 .连结
.连结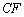 交
交
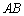 于点
于点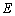 .
.
求证: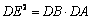 .
.
B. 选修4-2:矩阵与变换
求矩阵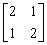 的特征值及对应的特征向量.
的特征值及对应的特征向量.
C. 选修4-4:坐标系与参数方程
已知曲线 的极坐标方程是
的极坐标方程是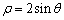 ,直线
,直线 的参数方程是
的参数方程是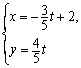 (
(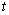 为参数).
为参数).
(1)将曲线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)设直线 与
与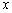 轴的交点是
轴的交点是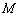 ,
,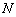 是曲线
是曲线 上一动点,求
上一动点,求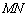 的最大值.
的最大值.
D.选修4-5:不等式选讲
设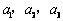 均为正数,且
均为正数,且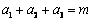 ,求证
,求证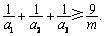
A. 选修4-1:几何证明选讲
【证明】连结OF.
因为DF切⊙O于F,所以∠OFD=90°.
所以∠OFC+∠CFD=90°.
因为OC=OF,所以∠OCF=∠OFC.
因为CO⊥AB于O,所以∠OCF+∠CEO=90°. ………………………5分
所以∠CFD=∠CEO=∠DEF,所以DF=DE.
因为DF是⊙O的切线,所以DF2=DB·DA.所以DE2=DB·DA. ……………10分
B. 选修4-2:矩阵与变换
【解】特征多项式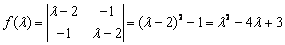 , …………3分
, …………3分
由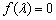 ,解得
,解得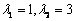 .
………………………………………6分
.
………………………………………6分
将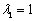 代入特征方程组,得
代入特征方程组,得 .
.
可取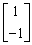 为属于特征值
为属于特征值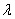 1=1的一个特征向量.
…………………………8分
1=1的一个特征向量.
…………………………8分
将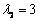 代入特征方程组, 得
代入特征方程组, 得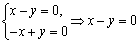 .
.
可取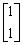 为属于特征值
为属于特征值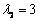 的一个特征向量.
的一个特征向量.
综上所述,矩阵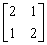 有两个特征值
有两个特征值 ;属于
;属于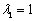 的一个特征向量为
的一个特征向量为 ,
,
属于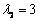 的一个特征向量为
的一个特征向量为 . ………………………………10分
. ………………………………10分
C. 选修4-4:坐标系与参数方程
【解】(1)曲线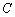 的极坐标方程可化为
的极坐标方程可化为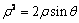 . ……………………2分
. ……………………2分
又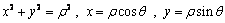 ,
,
所以曲线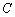 的直角坐标方程为
的直角坐标方程为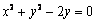 . ………………………4分
. ………………………4分
(2)将直线l的参数方程化为直角坐标方程,得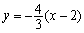 .…………………6分
.…………………6分
令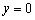 ,得
,得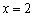 ,即
,即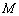 点的坐标为(2,0).
点的坐标为(2,0).
又曲线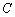 为圆,圆
为圆,圆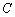 的圆心坐标为(1,0),半径
的圆心坐标为(1,0),半径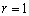 ,则
,则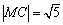 .
…………8分
.
…………8分
所以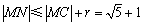 . ………………………………10分
. ………………………………10分
D.选修4-5:不等式选讲
【证明】因为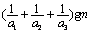
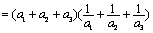
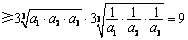 ,
,
当且仅当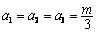 时等号成立.
时等号成立.
又因为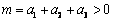 ,
,
所以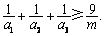 ……………10分
……………10分

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长.
 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长. ,其中
,其中 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的极坐标方程为
的极坐标方程为 ,
,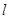 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长. ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程; 满足
满足 ,求
,求 的最小值;
的最小值; 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长.
 如图,
如图, 是边长为
是边长为 的正方形,以
的正方形,以 为圆心,
为圆心, 为半径的圆弧与以
为半径的圆弧与以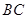 为直径的半⊙O交于点
为直径的半⊙O交于点 ,延长
,延长 交
交 于
于 .
. 的长.
的长. ,其中
,其中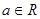 ,若点
,若点 在矩阵A的变换下得到
在矩阵A的变换下得到 .
. 的极坐标方程为
的极坐标方程为 ,
, 与圆相交于
与圆相交于 ,A两点,且∠
,A两点,且∠ ,求
,求 的长.
的长. ,且与圆相切的直线的极坐标方程;
,且与圆相切的直线的极坐标方程; 满足
满足 ,求
,求 的最小值;
的最小值;