摘要：20． 解:(Ⅰ)由.得 则 ---2分 .∴当时.,当时.. ∴当时.取得最大值．----4分 (Ⅱ)由题意知.即-5分 ∴ --6分 检验知.时.结论也成立.故.----7分 所以.令.则. 由(Ⅰ)可知. . ∴对任意的.不等式成立. ---9分 知.对任意的.有 ．-10分 令.则 --12分 则． ∴原不等式成立．-14分
网址：http://m.1010jiajiao.com/timu3_id_534175[举报]
（本小题满分14分）
设数列
是公差为
的等差数列，其前
项和为
．
（1）已知
，
，
（ⅰ）求当
时，
的最小值；
（ⅱ）当时，求证：
；
（2）是否存在实数
，使得对任意正整数，关于
的不等式
的最小正整数解为
?若存在，则求的取值范围；若不存在，则说明理由．
（本小题满分14分）
设数列
是公差为
的等差数列，其前
项和为
．
（1）已知
，
，
（ⅰ）求当
时，
的最小值；
（ⅱ）当时，求证：
；
（2）是否存在实数
，使得对任意正整数，关于
的不等式
的最小正整数解为
?若存在，则求的取值范围；若不存在，则说明理由．
（本小题满分14分）
设数列
是公差为
的等差数列，其前
项和为
．
（1）已知
，
，
（ⅰ）求当
时，
的最小值；
（ⅱ）当时，求证：
；
（2）是否存在实数
，使得对任意正整数，关于
的不等式
的最小正整数解为
?若存在，则求的取值范围；若不存在，则说明理由．
是公差为
的等差数列，其前
项和为
．
，
，
时，
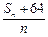的最小值；
；
，使得对任意正整数
的不等式
的最小正整数解为
?若存在，则求
是公差为
的等差数列，其前
项和为
．
，
，
时，
的最小值；
；
，使得对任意正整数
的不等式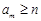
的最小正整数解为
?若存在，则求