摘要：19． 在四面体ABCD中.△BDC是等腰直角三角形.∠BDC=90°.BC=1.平面ABD与平面BDC垂直.且∠ABD= (1)证明:AB⊥CD, (2)求AC与BD所成的角, (3)求B到平面ACD的距离. 20090525
网址：http://m.1010jiajiao.com/timu3_id_534048[举报]
.（本
小题满分12分）
如图甲，在平面四边形ABCD中，已知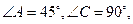
,
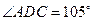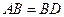,现将四边形ABCD沿BD折起，使平面ABD
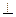平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．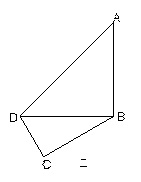
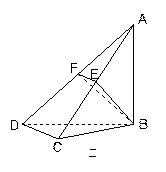
（1）求证：DC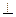平面ABC；
（2）设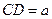
，求三棱锥A－BFE的体积．
（本小题满分12分）
如图甲，在平面四边形ABCD中，已知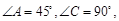
,
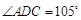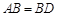,现将四边形ABCD沿BD折起，使平面ABD
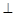平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
（Ⅰ）求证：DC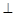平面ABC；
（Ⅱ）设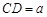
，求三棱锥A－BFE的体积．
查看习题详情和答案>>
（本小题满分12分）如图甲，在平面四边形ABCD中，已知
,
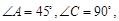
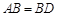,现将四边形ABCD沿BD折起，使平面ABD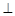
平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
（Ⅰ）求证：DC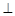平面ABC；
（Ⅱ）设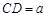
，求三棱锥A－BFE的体积．
查看习题详情和答案>>
,
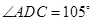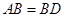,现将四边形ABCD沿BD折起，使平面ABD
平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
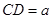，求三棱锥A－BFE的体积．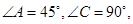
,
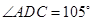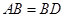,现将四边形ABCD沿BD折起，使平面ABD
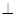平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
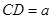，求三棱锥A－BFE的体积．