摘要:21.已知函数 f (x) = x3 -(l-3)x2 -(l +3)x + l -1在区间[n, m]上为减函数.记m的最大值为m0.n的最小值为n0.且满足m0-n0 = 4. (1)求m0.n0的值以及函数f (x)的解析式, (2)已知等差数列{xn}的首项x1 = .公差d = .又过点A(0, f (0)).B(1, f (1))的直线方程为y=g(x).试问:在数列{xn}中.哪些项满足f (xn)>g(xn)? (3)若对任意x1.x2Î[a, m0](x1 ¹ x2).都有成立.求a的最小值. 华南师大附中高三综合测试
网址:http://m.1010jiajiao.com/timu3_id_533902[举报]
已知函数 f (x) = x3 -(l-3)x2 -(l +3)x + l -1(l > 0)在区间[n, m]上为减函数,记m的最大值为m0,n的最小值为n0,且满足m0-n0 = 4. 
 (1)求m0,n0的值以及函数f (x)的解析式;
(1)求m0,n0的值以及函数f (x)的解析式;![]()
(2)已知等差数列{xn}的首项![]() .又过点A(0, f (0)),B(1, f (1))的直线方程为y=g(x).试问:在数列{xn}中,哪些项满足f (xn)>g(xn)?
.又过点A(0, f (0)),B(1, f (1))的直线方程为y=g(x).试问:在数列{xn}中,哪些项满足f (xn)>g(xn)?
(3)若对任意x1,x2∈ [a, m0](x1≠x2),都有![]() 成立,求a的最小值.
成立,求a的最小值.
已知函数f(x)=x3+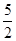 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+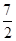 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数).
(1)若g(x)在x=l处的切线方程为y=kx-5(k为常数),求b的值;
(2)设函数f(x)的导函数为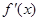 ,若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
,若存在唯一的实数x0,使得f(x0)=x0与f′(x0)=0同时成立,求实数b的取值范围;
(3)令F(x)=f(x)-g(x),若函数F(x)存在极值,且所有极值之和大于5+1n2,求a的取值范围.
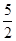 x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+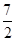 x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数). x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+ x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数).