题目内容
已知函数 f (x) = x3 -(l-3)x2 -(l +3)x + l -1(l > 0)在区间[n, m]上为减函数,记m的最大值为m0,n的最小值为n0,且满足m0-n0 = 4. 
 (1)求m0,n0的值以及函数f (x)的解析式;
(1)求m0,n0的值以及函数f (x)的解析式;![]()
(2)已知等差数列{xn}的首项![]() .又过点A(0, f (0)),B(1, f (1))的直线方程为y=g(x).试问:在数列{xn}中,哪些项满足f (xn)>g(xn)?
.又过点A(0, f (0)),B(1, f (1))的直线方程为y=g(x).试问:在数列{xn}中,哪些项满足f (xn)>g(xn)?
(3)若对任意x1,x2∈ [a, m0](x1≠x2),都有![]() 成立,求a的最小值.
成立,求a的最小值.
(1)![]() m0 = 3,n0 = -1
m0 = 3,n0 = -1
(2)当n< 91或n > 191(n∈N*)时,满足题意.
(3)a的最小值为1.
解析:
(1)![]() ,
,![]()
由题意可知m0,n0为方程f ′(x) = 0的两根.![]()
∴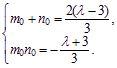 其中m0 > n0.
其中m0 > n0.
∵m0-n0 = 4,∴![]() = 4,即
= 4,即![]() = 0.
= 0.
解得l = 6或l = -3,∵l > 0,∴l = 6, ∴f (x) = x3 - 3x2 - 9x + 5.
同时可解得:m0 = 3,n0 = -1
(2)由(Ⅰ)得A(0, 5),B(1, -6),∴g(x) = -11x + 5.
∴![]() =
=![]() =
=![]() =
=![]() .
.
∵![]() >0,∴
>0,∴![]() .
.
由题意,得![]() .
.![]()
若![]() ,则
,则![]() ,∴n < 91.
,∴n < 91.
若![]() ,则
,则![]() ,∴n > 191.
,∴n > 191.
∴当n< 91或n > 191(n∈N*)时,满足题意.
(3)由(1)有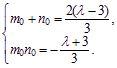 及l = 6, 易解得m0 = 3,n0 = -1.
及l = 6, 易解得m0 = 3,n0 = -1.
![]()
=![]() -
-![]()
=![]() +
+![]() =
=![]() .
.
由题意,![]() < 0恒成立,∴
< 0恒成立,∴![]() 恒成立.
恒成立.
∵m0 = 3,∴a≤x1<x2≤3.∴![]() .
.
要使![]() 恒成立,只要2a≥2,即a≥1.∴a的最小值为1.
恒成立,只要2a≥2,即a≥1.∴a的最小值为1.

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|