摘要:21. 已知:点A(0,1),点R在y轴上运动, 点T在x轴上,N为动点,且 (1)设动点N的轨迹为曲线C.求曲线C的方程, (2)如图所示:过点B的直线与曲线C交于点P.Q. 若在曲线C上存在点M.使得是以PQ为斜边的直角三角形.求直线的斜率的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_533707[举报]
(本小题满分12分)
已知M(-3,0)﹑N(3,0),P为坐标平面上的动点,且直线PM与直线PN的斜率之积为常数m(m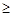 -1,m
-1,m 0).
0).
(1)求P点的轨迹方程并讨论轨迹是什么曲线?
(2)若 , P点的轨迹为曲线C,过点Q(2,0)斜率为
, P点的轨迹为曲线C,过点Q(2,0)斜率为 的直线
的直线 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为 ,求证
,求证 为定值;
为定值;
(3)在(2)的条件下,设 ,且
,且 ,求
,求 在y轴上的截距的变化范围.
在y轴上的截距的变化范围.

查看习题详情和答案>>
(本小题满分12分)
已知M(-3,0)﹑N(3,0),P为坐标平面上的动点,且直线PM与直线PN的斜率之积为常数m(m -1,m
-1,m 0).
0).
(1)求P点的轨迹方程并讨论轨迹是什么曲线?
(2)若 , P点的轨迹为曲线C,过点Q(2,0)斜率为
, P点的轨迹为曲线C,过点Q(2,0)斜率为 的直线
的直线 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为 ,求证
,求证 为定值;
为定值;
(3)在(2)的条件下,设 ,且
,且 ,求
,求 在y轴上的截距的变化范围.
在y轴上的截距的变化范围.

已知M(-3,0)﹑N(3,0),P为坐标平面上的动点,且直线PM与直线PN的斜率之积为常数m(m
 -1,m
-1,m 0).
0).(1)求P点的轨迹方程并讨论轨迹是什么曲线?
(2)若
 , P点的轨迹为曲线C,过点Q(2,0)斜率为
, P点的轨迹为曲线C,过点Q(2,0)斜率为 的直线
的直线 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR(O为坐标原点)的斜率为 ,求证
,求证 为定值;
为定值;(3)在(2)的条件下,设
 ,且
,且 ,求
,求 在y轴上的截距的变化范围.
在y轴上的截距的变化范围.
(本小题满分12分)已知二次函数f(x)=ax2+bx+c.
(1)若f(-1)=0,试判断函数f(x)零点的个数;
(2)是否存在a,b,c∈R,使f(x)同时满足以下条件:
①对任意x∈R,f(-1+x)=f(-1-x),且f(x)≥0;
②对任意x∈R,都有0≤f(x)-x≤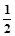 (x-1)2.若存在,求出a,b,c的值;若不存在,请说
(x-1)2.若存在,求出a,b,c的值;若不存在,请说
明理由。
(3)若对任意x1、x2∈R且x1<x2,f(x1)≠f(x2),试证明:存在x0∈(x1,x2),使f(x0)=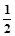 [f(x1)+f(x2)]成立。
[f(x1)+f(x2)]成立。
查看习题详情和答案>>

 时,求f(x)的不动点;
时,求f(x)的不动点;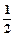 (x-1)2.若存在,求出a,b,c的值;若不存在,请说
(x-1)2.若存在,求出a,b,c的值;若不存在,请说