摘要:(命题人:如东丰利中学花龙泉. 审题人:如东丰利中学朱兵) 已知向量.动点M到定直线的距离等于.并且满足.其中O为坐标原点.K为参数, (1)求动点M的轨迹方程.并判断曲线类型, (2)当k=时.求的最大值和最小值, 的条件下.将曲线向左平移一个单位.在x轴上是否存在一点P(m.0)使得过点P的直线交该曲线于D.E两点.并且以DE为直径的圆经过原点.若存在.请求出的最小值,若不存在.请说明理由. [解析](1)设.则由. 且O为原点得A 从而 代入得 为所求轨迹方程 当K=1时.=0 轨迹为一条直线 当K1时..若K=0.则为圆 ,若K.则为双曲线 (2)当K=时.若或则为椭圆 方程为.即且 从而 又 当时.取最小值.当 时.取最大值16 故. 的条件下.将曲线向左平移一个单位后曲线方程为 假设存在过P(m,0)直线满足题意条件.不妨设过P(m,0)直线方程为 设D(x1,y1 ),E(x2,y2 ). 消去x得: 即 由韦达定理.得 由于以DE为直径的圆都过原点则,即 又因为 即显然能满足 故当
网址:http://m.1010jiajiao.com/timu3_id_533663[举报]
已知向量 ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足 ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数.
(1)求动点M的轨迹方程,并判断曲线类型;
(2)当 时,求
时,求 的最大值和最小值;
的最大值和最小值;
(3)如果动点M的轨迹是圆锥曲线,其离心率e满足 ,求实数k的取值范围.
,求实数k的取值范围.
查看习题详情和答案>>
 ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足 ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数.(1)求动点M的轨迹方程,并判断曲线类型;
(2)当
 时,求
时,求 的最大值和最小值;
的最大值和最小值;(3)如果动点M的轨迹是圆锥曲线,其离心率e满足
 ,求实数k的取值范围.
,求实数k的取值范围.查看习题详情和答案>>
已知向量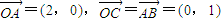 ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足 ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数.
(1)求动点M的轨迹方程,并判断曲线类型;
(2)当 时,求
时,求 的最大值和最小值;
的最大值和最小值;
(3)如果动点M的轨迹是圆锥曲线,其离心率e满足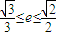 ,求实数k的取值范围.
,求实数k的取值范围.
查看习题详情和答案>>
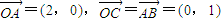 ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足 ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数.(1)求动点M的轨迹方程,并判断曲线类型;
(2)当
 时,求
时,求 的最大值和最小值;
的最大值和最小值;(3)如果动点M的轨迹是圆锥曲线,其离心率e满足
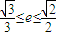 ,求实数k的取值范围.
,求实数k的取值范围.查看习题详情和答案>>
已知向量 ,动点M到定直线
,动点M到定直线 的距离等于
的距离等于 ,并且满足
,并且满足 ,其中
,其中 为坐标原点,
为坐标原点, 为非负实数.
为非负实数.
(I)求动点M的轨迹方程 ;
;
(II)若将曲线 向左平移一个单位,得曲线
向左平移一个单位,得曲线 ,试判断曲线
,试判断曲线 为何种类型;
为何种类型;
(III)若(II)中曲线 为圆锥曲线,其离心率满足
为圆锥曲线,其离心率满足 ,当
,当 是曲线
是曲线 的两个焦点时,则曲线
的两个焦点时,则曲线 上恒存在点P,使得
上恒存在点P,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看习题详情和答案>>
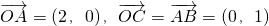 ,动点M到定直线y=1的距离等于d,并且满足
,动点M到定直线y=1的距离等于d,并且满足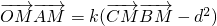 ,其中O是坐标原点,k是参数.
,其中O是坐标原点,k是参数. 时,求
时,求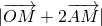 的最大值和最小值;
的最大值和最小值;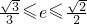 ,求实数k的取值范围.
,求实数k的取值范围.