摘要:21. (选题人:启东中学徐建明.审题人:启东中学李俊) 设A(x1.y1).B(x2.y2)是函数f(x)=的图象上任意两点.且.已知点M的横坐标为. (1)求证:M点的纵坐标为定值, (2)若Sn=f(∈N*.且n≥2.求Sn. (3)已知an=其中n∈N*. Tn为数列{an}的前n项和.若Tn<λ(Sn+1+1)对一切n∈N*都成立.试求λ的取值范围. [解析](1)证明:∵ ∴M是AB的中点.设M点的坐标为(x.y). 由(x1+x2)=x=.得x1+x2=1.则x1=1-x2或x2=1-x1. 而y=(y1+y2)= [f(x1)+f(x2)] =(+log2 =(1+log2 =(1+log2 =(1+log2∴M点的纵坐标为定值. .知x1+x2=1.f(x1)+f(x2)=y1+y2=1. Sn=f(Sn=f(. 两式相加.得 2Sn=[f()+[f()+-+[f() = .∴Sn=(n≥2.n∈N*). (3)当n≥2时.an= Tn=a1+a2+a3+-+an=[(] =( 由Tn<λ(Sn+1+1).得<λ·∴λ> ∵n+≥4.当且仅当n=2时等号成立.∴ 因此λ>.即λ的取值范围是(+∞).
网址:http://m.1010jiajiao.com/timu3_id_533643[举报]
(本题满分16分)A、B是函数f(x)=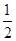 +
+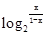 的图象上的任意两点,且
的图象上的任意两点,且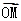 =
=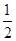 (
(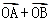 ),已知点M的横坐标为
),已知点M的横坐标为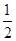 .
.
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f(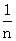 )+f(
)+f(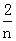 )+…+f(
)+…+f(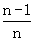 ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;
(Ⅲ)已知数列{an}的通项公式为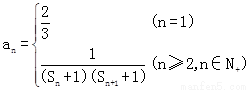 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn<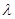 (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数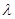 的取值范围.
的取值范围.
查看习题详情和答案>>
(本题满分16分)A、B是函数f(x)= +
+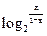 的图象上的任意两点,且
的图象上的任意两点,且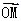 =
= (
(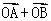 ),已知点M的横坐标为
),已知点M的横坐标为 .
.
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f( )+f(
)+f( )+…+f(
)+…+f(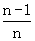 ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;
(Ⅲ)已知数列{an}的通项公式为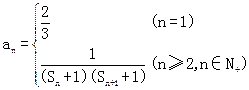 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn<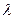 (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数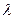 的取值范围.
的取值范围.
A、B是函数f(x)=![]() +
+![]() 的图象上的任意两点,且
的图象上的任意两点,且![]() =
=![]() (
(![]() ),已知点M的横坐标为
),已知点M的横坐标为![]() .
.
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f(![]() )+f(
)+f(![]() )+…+f(
)+…+f(![]() ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;
(Ⅲ)已知数列{an}的通项公式为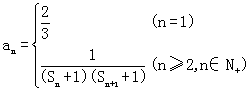 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn<![]() (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数![]() 的取值范围.
的取值范围.
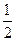 +
+ 的图象上的任意两点,且
的图象上的任意两点,且 =
= ),已知点M的横坐标为
),已知点M的横坐标为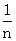 )+f(
)+f( )+…+f(
)+…+f( ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn; . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn< (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数