摘要：20． (选题人:启东中学陈兵.审题人:启东中学李俊) 已知定理:“若为常数.满足.则函数的图象关于点中心对称 ．设函数.定义域为A． (1)试证明的图象关于点成中心对称, (2)当时.求证:, (3)对于给定的.设计构造过程:.-.．如果.构造过程将继续下去,如果.构造过程将停止．若对任意.构造过程可以无限进行下去.求a的值． [解析](1)∵.∴． 由已知定理.得的图象关于点成中心对称． (2)先证明在上是增函数.只要证明在上是增函数． 设.则. ∴在上是增函数． 再由在上是增函数.得 当时..即． (3)∵构造过程可以无限进行下去.∴对任意恒成立． ∴方程无解.即方程无解或有唯一解． ∴或由此得到．
网址：http://m.1010jiajiao.com/timu3_id_533642[举报]
（本小题满分12分）
已知定理：若“
为常数，
满足
，则函数
的图象关于点
中心对称。”设函数
，定义域为A。
（1）证明：函数
的图象关于点
中心对称；
（2）当
时，求函数值
的取值范围；
（3）对于给定的
，设计构造过程：
，若
，构造过程将继续下去；若
，构造过程都可以无限进行下去，求
的值。
已知定理：“若a，b为常数，g（x）满足g（a+x）+g（a-x）=2b，则函数y=g（x）的图象关于点（a，b）中心对称”．设函数f(x)=
，定义域为A．
（1）试证明y=f（x）的图象关于点（a，-1）成中心对称；
（2）当x∈[a-2，a-1]时，求证：f(x)∈[-
， 0]；
（3）对于给定的x1∈A，设计构造过程：x2=f（x1），x3=f（x2），…，xn+1=f（xn）．如果xi∈A（i=2，3，4…），构造过程将继续下去；如果xi∉A，构造过程将停止．若对任意x1∈A，构造过程都可以无限进行下去，求a的值． 查看习题详情和答案>>
| x+1-a |
| a-x |
（1）试证明y=f（x）的图象关于点（a，-1）成中心对称；
（2）当x∈[a-2，a-1]时，求证：f(x)∈[-
| 1 |
| 2 |
（3）对于给定的x1∈A，设计构造过程：x2=f（x1），x3=f（x2），…，xn+1=f（xn）．如果xi∈A（i=2，3，4…），构造过程将继续下去；如果xi∉A，构造过程将停止．若对任意x1∈A，构造过程都可以无限进行下去，求a的值． 查看习题详情和答案>>
已知定理：“若a，b为常数，g（x）满足g（a+x）+g（a-x）=2b．则函数y=g（x）的图象关于点（a，b）成中心对称”．设函数f（x）=
，定义域为A．
（1）试证明y=f（x）的图象关于点（a，-1）成中心对称；
（2）写出f（x）的单调区间（不证明），并求当x∈[a-2，a-1]时，函数f（x）的值域；
（3）对于给定的x1∈A，设计构造过程：x2=f（x1），x3=f（x2），…，xn+1=f（xn）．如果xi∈A（i=1，2，3，4…），构造过程将继续下去；如果xi∉A，构造过程将停止．若对任意x1∈A，构造过程都可以无限进行下去，求a的值．
查看习题详情和答案>>
| x+1-a | a-x |
（1）试证明y=f（x）的图象关于点（a，-1）成中心对称；
（2）写出f（x）的单调区间（不证明），并求当x∈[a-2，a-1]时，函数f（x）的值域；
（3）对于给定的x1∈A，设计构造过程：x2=f（x1），x3=f（x2），…，xn+1=f（xn）．如果xi∈A（i=1，2，3，4…），构造过程将继续下去；如果xi∉A，构造过程将停止．若对任意x1∈A，构造过程都可以无限进行下去，求a的值．
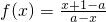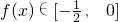，定义域为A．
；
，定义域为A．
；