摘要：9． (命题人:如东中学唐勇.审题人:如东中学何鹏.由2008年第2期题 目改编 ) 打开“几何画板 软件进行如下操作: ①用画图工具在工作区画一个大小适中的圆C, ②用取点工具分别在圆C上和圆C外各取一个点A.B, ③用构造菜单下对应命令作出线段AB的垂直平分线l, ④作出直线AC． 设直线AC与直线l相交于点P.当点A在圆C上运动时.点P的轨迹是 ． [解析]双曲线．由图可得.PC-PB＝PC-PA＝AC.或PB-PC＝PA-PC＝AC. 从而点P到定点B.C的距离之差的绝对值是定长AC.由双曲线定义即可得．
网址：http://m.1010jiajiao.com/timu3_id_533631[举报]
打开“几何画板”软件进行如下操作：
①用画图工具在工作区画一个大小适中的图C；
②用取点工具分别在圆C上和圆C外各取一个点A，B；
③用构造菜单下对应命令作出线段AB的垂直平分线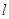
；
④作出直线AC。
设直线AC与直线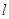相交于点P，当点B为定点，点A在圆C上运动时，点P的轨迹是（ ）
A、椭圆 B、双曲线 C、抛物线 D、圆
查看习题详情和答案>>
打开“几何画板”软件进行如下操作：
①用画图工具在工作区画一个大小适中的图C；
②用取点工具分别在圆C上和圆C外各取一个点A，B；
③用构造菜单下对应命令作出线段AB的垂直平分线l；
④作出直线AC．设直线AC与直线l相交于点P，当点B为定点，点A在圆C上运动时，点P的轨迹是
- A.椭圆
- B.双曲线
- C.抛物线
- D.圆
打开“几何画板”软件进行如下操作：
①用画图工具在工作区画一个大小适中的图C；
②用取点工具分别在圆C上和圆C外各取一个点A，B；
③用构造菜单下对应命令作出线段AB的垂直平分线
；
④作出直线AC。
设直线AC与直线相交于点P，当点B为定点，点A在圆C上运动时，点P的轨迹是（ ）
A、椭圆 
B、双曲线 C、抛物线 D、圆
（08年内江市三模） 打开“几何画板”进行如下操作：
①用画图工具在工作区画一个圆C；（C为圆心）
②用取点工具分别在圆C上和圆外各取一点A、B；
③用构造菜单下对应命令作出线段AB的垂直平分线
；
④作直线AC
设直线AC与相交于点P，当A在圆C上运动时，P点的轨迹是
A、抛物线 B、椭圆 C、双曲线 D、直线
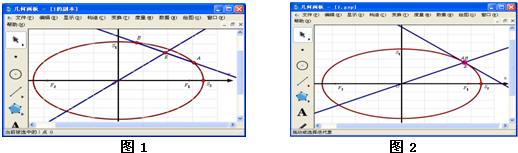
查看习题详情和答案>>某同学用《几何画板》研究椭圆的性质：打开《几何画板》软件，绘制某椭圆C1：
+
=1，在椭圆上任意画一个点S，度量点S的坐标（xs，ys），如图1．
（1）拖动点S，发现当xs=
时，ys=0；当xs=0时，ys=1，试求椭圆C1的方程；
（2）该同学知圆具有性质：若E为圆O：x2+y2=r2（r＞0）的弦AB的中点，则直线AB的斜率kAB与直线OE的斜率kOE的乘积kAB•kOE为定值．该同学在椭圆上构造两个不同的点A、B，并构造直线AB，再构造AB的中点E，经观察得：沿着椭圆C1，无论怎样拖动点A、B，椭圆也具有此性质．类比圆的这个性质，请写出椭圆C1的类似性质，并加以证明；
（3）拖动点A、B的过程中，如图2发现当点A与点B在C1在第一象限中的同一点时，直线AB刚好为C1的切线l，若l分别与x轴和y轴的正半轴交于C，D两点，求三角形OCD面积的最小值．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
（1）拖动点S，发现当xs=
| 2 |
（2）该同学知圆具有性质：若E为圆O：x2+y2=r2（r＞0）的弦AB的中点，则直线AB的斜率kAB与直线OE的斜率kOE的乘积kAB•kOE为定值．该同学在椭圆上构造两个不同的点A、B，并构造直线AB，再构造AB的中点E，经观察得：沿着椭圆C1，无论怎样拖动点A、B，椭圆也具有此性质．类比圆的这个性质，请写出椭圆C1的类似性质，并加以证明；
（3）拖动点A、B的过程中，如图2发现当点A与点B在C1在第一象限中的同一点时，直线AB刚好为C1的切线l，若l分别与x轴和y轴的正半轴交于C，D两点，求三角形OCD面积的最小值．