摘要:6. (命题人:启东中学顾晏辉.审题人:启东中学李俊) 己知:函数满足.又.则函数的解析式为 . [解析]由已知.当时.原方程化为. 由等式右边存在极限.处处可导. 对原方程两边令.得. 令.(为常数). 又.得.
网址:http://m.1010jiajiao.com/timu3_id_533628[举报]
己知实数m≠0,又
=(x2-1,mx),
=(mx,
),设函数f(x)=
•
.
(1)若m>0,且f(-2)=f(2),求m的值;
(2)若对一切正整数k,有f(2k)>f(2k-1),求m的取值范围.
查看习题详情和答案>>
| a |
| b |
| 1 |
| m |
| a |
| b |
(1)若m>0,且f(-2)=f(2),求m的值;
(2)若对一切正整数k,有f(2k)>f(2k-1),求m的取值范围.
(2013•绵阳二模)已知函数f(x)=xlnx(x∈(0,+∞)
(I )求g(x)=
-x(x∈(-1,+∞))的单调区间与极大值;
(II )任取两个不等的正数x1,x2,且x1<x2,若存在x0>0使f′(x0)=
成立,求证:x1<x0<x2
(III)己知数列{an}满足a1=1,an+1=(1+
)an+
(n∈N+),求证:an<e
(e为自然对数的底数).
查看习题详情和答案>>
(I )求g(x)=
| f(x+1) |
| x+1 |
(II )任取两个不等的正数x1,x2,且x1<x2,若存在x0>0使f′(x0)=
| f(x2)-f(x1) |
| x2-x1 |
(III)己知数列{an}满足a1=1,an+1=(1+
| 1 |
| 2n |
| 1 |
| n2 |
| 11 |
| 4 |
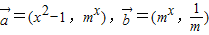 ,设函数
,设函数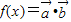 .
.