摘要：已知抛物线.圆.P.Q分别为曲线E和曲线C上的点.则的最小值为 A．1 B． C． D．
网址：http://m.1010jiajiao.com/timu3_id_533033[举报]
已知F1、F2分别是椭圆
+
=1的左、右焦点，曲线C是以坐标原点为顶点，以F2为焦点的抛物线，自点F1引直线交曲线C于P、Q两个不同的点，点P关于x轴对称的点记为M，设
=λ
．
（1）写出曲线C的方程；
（2）若
=u
，试用λ表示u；
（3）若λ∈[2，3]，求|PQ|的取值范围．
查看习题详情和答案>>
| x2 |
| 4 |
| y2 |
| 3 |
| F1P |
| F1Q |
（1）写出曲线C的方程；
（2）若
| F2M |
| F2Q |
（3）若λ∈[2，3]，求|PQ|的取值范围．
已知椭圆以坐标原点为中心，坐标轴为对称轴，且该椭圆以抛物线y2=16x的焦点P为其一个焦点，以双曲线
-
=1的焦点Q为顶点．
（1）求椭圆的标准方程；
（2）已知点A（-1，0），B（1，0），且C、D分别为椭圆的上顶点和右顶点，点M是线段CD上的动点，求
•
的取值范围．
查看习题详情和答案>>
| x2 |
| 16 |
| y2 |
| 9 |
（1）求椭圆的标准方程；
（2）已知点A（-1，0），B（1，0），且C、D分别为椭圆的上顶点和右顶点，点M是线段CD上的动点，求
| AM |
| BM |
(本小题满分14分)
已知F1，F2分别是椭圆＋＝1的左、右焦点，曲线C是以坐标原点为顶点，以F2为焦点的抛物线，自点F1引直线交曲线C于P、Q两个不同的交点，点P关于x轴的对称点记为M.设＝λ.
(Ⅰ)求曲线C的方程；
(Ⅱ)证明：＝－λ；
(Ⅲ)若λ∈[2,3]，求|PQ|的取值范围.
查看习题详情和答案>>
的左、右顶点分别为A、B，椭圆C的右焦点为F，过F作一条垂直于x轴的直线与椭圆相交于R、S，若线段RS的长为
．
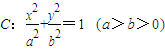的左、右顶点分别为A、B，椭圆C的右焦点为F，过F作一条垂直于x轴的直线与椭圆相交于R、S，若线段RS的长为
．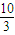