摘要：21．(理)如图.|AB|=2.O为AB中点.直线过B且垂直于AB.过A的动直线与交于点C.点M在线段AC上.满足=. (1)求点M的轨迹方程, (2)若过B点且斜率为- 的直线与轨迹M交于 点P.点Q(t,0)是x轴上任意一点.求当 ΔBPQ为锐角三角形时t的取值范围．
网址：http://m.1010jiajiao.com/timu3_id_532762[举报]
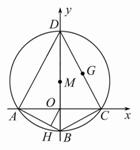
（理）如图，|AB|=2，O为AB中点，直线
过B且垂直于AB，过A的动直线与交于点C，点M在线段AC上，满足
=
.
（1）求点M的轨迹方程；
（2）若过B点且斜率为- 
的直线与轨迹M交于点P，点Q(t,0)是x轴上任意一点，求当ΔBPQ为锐角三角形时t的取值范围．
查看习题详情和答案>>
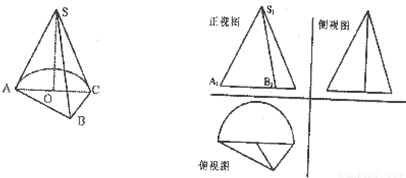
如图，几何体SABC的底面是由以AC为直径的半圆O与△ABC组成的平面图形，SO⊥平面ABC，AB⊥BC，SA=SB=SC=A C=4，BC=2．（l）求直线SB与平面SAC所成角的正弦值；
（2）求几何体SABC的正视图中△S1A1B1的面积；
（3）试探究在圆弧AC上是否存在一点P，使得AP⊥SB，若存在，说明点P的位置并证明；若不存在，说明理由．
如图，已知四棱锥S—ABCD的底面是边长为4的正方形,S在底面的射影O在正方形ABCD内,且O到AB,AD的距离分别为2和1.
(1)求证:
·
是定值;
(2)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为90°?若存在,请给出证明,并求出AQ的长;若不存在,请说明理由.
查看习题详情和答案>>
直角坐标系中，方程为x2＋y2＋Dx＋Ey＋F＝0的圆M的内接四边形ABCD的对角线AC和BD互相垂直，且AC和BD分别在x轴和y轴上.
＝0，求D2＋E2－4F的值；
