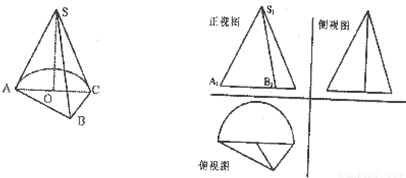
题目内容
 如图,几何体SABC的底面是由以AC为直径的半圆O与△ABC组成的平面图形,SO⊥平面ABC,AB⊥BC,SA=SB=SC=A C=4,BC=2.
如图,几何体SABC的底面是由以AC为直径的半圆O与△ABC组成的平面图形,SO⊥平面ABC,AB⊥BC,SA=SB=SC=A C=4,BC=2.(l)求直线SB与平面SAC所成角的正弦值;
(2)求几何体SABC的正视图中△S1A1B1的面积;
(3)试探究在圆弧AC上是否存在一点P,使得AP⊥SB,若存在,说明点P的位置并证明;若不存在,说明理由.
分析:(1)利用线面垂直的判定定理和性质定理及线面角的定义即可求出;
(2)由(1)可知:A1B1=AH,而可证明SO为高,进而即可求出面积;
(3)利用线面垂直的判定定理和性质定理及圆心角定理即可得出.
(2)由(1)可知:A1B1=AH,而可证明SO为高,进而即可求出面积;
(3)利用线面垂直的判定定理和性质定理及圆心角定理即可得出.
解答: 解:(1)如图1过点B作BH⊥AC于点H,连接SH.
解:(1)如图1过点B作BH⊥AC于点H,连接SH.
∵SO⊥平面ABC,BH?平面ABC,
∴BH⊥SO.
又SO∩AC=O,
∴BH⊥平面SAC,
即∠BSH就是直线SB与平面SAC所成角.
在△ABC中,∵AB⊥BC,AC=4,BC=2,
∴∠ACB=60°,BH=2sin60°=
.
在Rt△BSH中,∵SB=4,
∴sin∠BSH=
=
,
即直线SB与平面SAC所成角的正弦值为
.
(2)由(1)知,几何体SABC的正视图中,△S1A1B1的边A1
=AH=AC-HC,
而HC=2cos60°=1,∴A1
=3.
又△S1A1B1的边A1B1上的高等于几何体SABC中SO的长,而SA=SC=AC=4,∴SO=2
,
∴S△S1A1B1=
×3×2
=3
.
(3)存在.
证明如下:
如图2,连接BO并延长交弧AC于点M,
在底面内,过点A作AP⊥BM交弧AC于点P.
∵SO⊥平面ABC.
而AP?平面ABC,∴AP⊥SO.
又∵AP⊥BM,SO∩BM=O,
∴AP⊥平面SOB,从而AP⊥SB.
又∵AO=OC=BC=2,∴∠AOM=∠BOC=∠ACB=60°,
∴∠AOM=∠POM=60°,∠AOP=120°,
即点P位于弧AC的三等分的位置,且∠AOP=120°.
 解:(1)如图1过点B作BH⊥AC于点H,连接SH.
解:(1)如图1过点B作BH⊥AC于点H,连接SH.∵SO⊥平面ABC,BH?平面ABC,
∴BH⊥SO.
又SO∩AC=O,
∴BH⊥平面SAC,
即∠BSH就是直线SB与平面SAC所成角.
在△ABC中,∵AB⊥BC,AC=4,BC=2,
∴∠ACB=60°,BH=2sin60°=
| 3 |
在Rt△BSH中,∵SB=4,
∴sin∠BSH=
| BH |
| SB |
| ||
| 4 |
即直线SB与平面SAC所成角的正弦值为
| ||
| 4 |
(2)由(1)知,几何体SABC的正视图中,△S1A1B1的边A1
| B | 1 |
而HC=2cos60°=1,∴A1
| B | 1 |
又△S1A1B1的边A1B1上的高等于几何体SABC中SO的长,而SA=SC=AC=4,∴SO=2
| 3 |
∴S△S1A1B1=
| 1 |
| 2 |
| 3 |
| 3 |
(3)存在.
证明如下:
如图2,连接BO并延长交弧AC于点M,
在底面内,过点A作AP⊥BM交弧AC于点P.
∵SO⊥平面ABC.
而AP?平面ABC,∴AP⊥SO.
又∵AP⊥BM,SO∩BM=O,
∴AP⊥平面SOB,从而AP⊥SB.
又∵AO=OC=BC=2,∴∠AOM=∠BOC=∠ACB=60°,
∴∠AOM=∠POM=60°,∠AOP=120°,
即点P位于弧AC的三等分的位置,且∠AOP=120°.
点评:熟练掌握用线面垂直的判定定理和性质定理及线面角的定义、三角形的面积公式、圆心角定理是解题的关键.

练习册系列答案
相关题目