摘要： 在解决问题:“证明数集没有最小数 时.可用反证法证明． 假设是中的最小数.则取.可得:.与假设中“是中的最小数 矛盾! 那么对于问题:“证明数集没有最大数 .也可以用反证法证明．我们可以假设是中的最大数.则可以找到 (用.表示).由此可知..这与假设矛盾!所以数集没有最大数．
网址：http://m.1010jiajiao.com/timu3_id_532508[举报]
在解决问题：“证明数集
没有最小数”时，可用反证法证明．
假设
是
中的最小数，则取
，可得：
，与假设中“
是中的最小数”矛盾！ 那么对于问题：“证明数集
没有最大数”，也可以用反证法证明．我们可以假设
是
中的最大数，则可以找到
▲ （用
，
表示），由此可知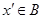
，
，这与假设矛盾！所以数集没有最大数．
查看习题详情和答案>>
在解决问题：“证明数集
没有最小数”时，可用反证法证明．
假设
是
中的最小数，则取
，可得：
，与假设中“
是中的最小数”矛盾！那么对于问题：“证明数集
没有最大数”，也可以用反证法证明．我们可以假设
是
中的最大数，则可以找到
▲ （用
，
表示），由此可知
，
，这与假设矛盾！所以数集没有最大数．
在解决问题：“证明数集
没有最小数”时，可用反证法证明．
假设
是
中的最小数，则取
，可得：
，与假设中“
是中的最小数”矛盾！那么对于问题：“证明数集
没有最大数”，也可以用反证法证明．我们可以假设
是
中的最大数，则可以找到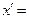
▲ （用
，
表示），由此可知
，
，这与假设矛盾！所以数集没有最大数．
没有最小数”时，可用反证法证明．假设
是中的最小数，则取，可得：，与假设中“是中的最小数”矛盾！那么对于问题：“证明数集没有最大数”，也可以用反证法证明．我们可以假设是中的最大数，则可以找到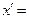 ▲ （用，表示），由此可知，，这与假设矛盾！所以数集没有最大数．
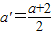，可得：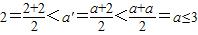
，与假设中“a是A中的最小数”矛盾！那么对于问题：“证明数集
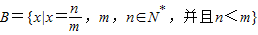没有最大数”，也可以用反证法证明．我们可以假设
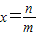是B中的最大数，则可以找到x'= （用m，n表示），由此可知x'∈B，x'＞x，这与假设矛盾！所以数集B没有最大数．