题目内容
在解决问题:“证明数集A={x|2<x≤3}没有最小数”时,可用反证法证明.假设a(2<a≤3)是A中的最小数,则取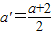 ,可得:
,可得: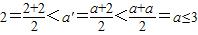 ,与假设中“a是A中的最小数”矛盾!那么对于问题:“证明数集
,与假设中“a是A中的最小数”矛盾!那么对于问题:“证明数集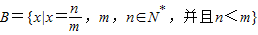 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设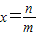 是B中的最大数,则可以找到x'= (用m,n表示),由此可知x'∈B,x'>x,这与假设矛盾!所以数集B没有最大数.
是B中的最大数,则可以找到x'= (用m,n表示),由此可知x'∈B,x'>x,这与假设矛盾!所以数集B没有最大数.
【答案】分析:利用不等式的性质可得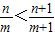 ,且n+1<m+1,n+1∈N*,m+1∈N*,故 x'=
,且n+1<m+1,n+1∈N*,m+1∈N*,故 x'=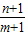 ,
,
从而得到答案.
解答:解:证明数集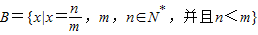 没有最大数”,可以用反证法证明.
没有最大数”,可以用反证法证明.
假设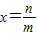 是B中的最大数,则可以找到x'=
是B中的最大数,则可以找到x'=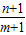 ,
,
,n+1<m+1,n+1∈N*,m+1∈N*,且x'>x,
这与假设矛盾!所以数集B没有最大数.
故答案为: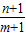 .
.
点评:本题主要考查用反证法证明数学命题,不等式的性质的应用.本题的答案不唯一,如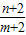 ,
,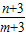 …都可以.
…都可以.
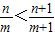 ,且n+1<m+1,n+1∈N*,m+1∈N*,故 x'=
,且n+1<m+1,n+1∈N*,m+1∈N*,故 x'=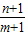 ,
,从而得到答案.
解答:解:证明数集
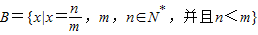 没有最大数”,可以用反证法证明.
没有最大数”,可以用反证法证明.假设
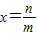 是B中的最大数,则可以找到x'=
是B中的最大数,则可以找到x'=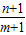 ,
,,n+1<m+1,n+1∈N*,m+1∈N*,且x'>x,
这与假设矛盾!所以数集B没有最大数.
故答案为:
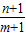 .
.点评:本题主要考查用反证法证明数学命题,不等式的性质的应用.本题的答案不唯一,如
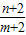 ,
,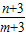 …都可以.
…都可以. 
练习册系列答案
相关题目
 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明. 是
是 中的最小数,则取
中的最小数,则取 ,可得:
,可得: ,与假设中“
,与假设中“ 是
是 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设 是
是 中的最大数,则可以找到
中的最大数,则可以找到 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知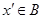 ,
, ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集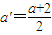 ,可得:
,可得: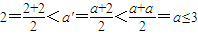 ,与假设中“a是A中的最小数”矛盾!那么对于问题:“证明数集
,与假设中“a是A中的最小数”矛盾!那么对于问题:“证明数集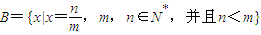 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设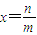 是B中的最大数,则可以找到x'= (用m,n表示),由此可知x'∈B,x'>x,这与假设矛盾!所以数集B没有最大数.
是B中的最大数,则可以找到x'= (用m,n表示),由此可知x'∈B,x'>x,这与假设矛盾!所以数集B没有最大数.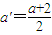 ,可得:
,可得: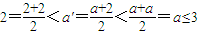 ,与假设中“a是A中的最小数”矛盾!那么对于问题:“证明数集
,与假设中“a是A中的最小数”矛盾!那么对于问题:“证明数集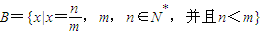 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设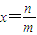 是B中的最大数,则可以找到x'= (用m,n表示),由此可知x'∈B,x'>x,这与假设矛盾!所以数集B没有最大数.
是B中的最大数,则可以找到x'= (用m,n表示),由此可知x'∈B,x'>x,这与假设矛盾!所以数集B没有最大数.