摘要:2.已知直线所经过的定点恰好是椭圆的一个焦点,且椭圆上的点到点的最大距离为8. (Ⅰ)求椭圆的标准方程, (Ⅱ)已知圆,直线.试证明当点在椭圆上运动时,直线与圆恒相交,并求直线被圆所截得的弦长的取值范围. 解: (Ⅰ)由,得, 则由,解得F(3,0). 设椭圆的方程为,则,解得 所以椭圆的方程为 (Ⅱ)因为点在椭圆上运动,所以, 从而圆心到直线的距离. 所以直线与圆恒相交 又直线被圆截得的弦长为 由于,所以,则, 即直线被圆截得的弦长的取值范围是
网址:http://m.1010jiajiao.com/timu3_id_531933[举报]
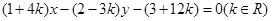 所经过的定点
所经过的定点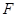 恰好是椭圆
恰好是椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆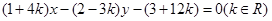 所经过的定点
所经过的定点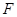 恰好是椭圆
恰好是椭圆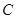 的一个焦点,且椭圆
的一个焦点,且椭圆