摘要：如图.某小区准备绿化一块直径为的半圆形空地.外的地方种草.的内接正方形为一水池,其余地方种花.若 ,设的面积为.正方形的面积为.将比值称为“规划合理度 . (1)①试用,表示 ②. 试用,表示 (2)当为定值.变化时,求“规划合理度 取得最小值时的角的大小. 解:(1). 如图.在ABC中 .＝ 设正方形的边长为 则 ＝(2). 而＝ 0 < < 又0 <2 < 当0<£1 为减函数 当时 取得最小值为此时
网址：http://m.1010jiajiao.com/timu3_id_531880[举报]
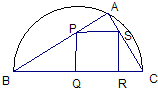（2007•杨浦区二模）如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值| S1 | S2 |
（1）试用a，θ表示S1和S2．
（2）（理）当a为定值，θ变化时，求“规划合理度”取得最小值时的角θ的大小．
（3）（文）当a为定值，θ=150时，求“规划合理度”的值．
如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值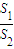
称为“规划合理度”．
（1）试用a，θ表示S1和S2．
（2）（理）当a为定值，θ变化时，求“规划合理度”取得最小值时的角θ的大小．
（3）（文）当a为定值，θ=15时，求“规划合理度”的值．
查看习题详情和答案>>
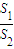称为“规划合理度”．（1）试用a，θ表示S1和S2．
（2）（理）当a为定值，θ变化时，求“规划合理度”取得最小值时的角θ的大小．
（3）（文）当a为定值，θ=15时，求“规划合理度”的值．
查看习题详情和答案>>
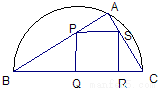
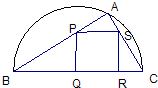如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值
称为“规划合理度”．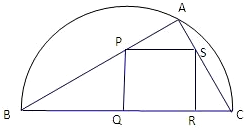
如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余地方种花．若BC=20米，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值
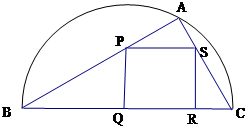如图，某小区准备绿化一块直径为BC的半圆形空地，△ABC的内接正方形PQRS为一水池，△ABC外的地方种草，其余地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2，将比值