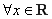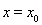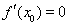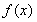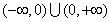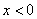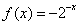摘要：解析:显然S1是正确的．假设后三个数均未算错.则a1=8.a2=12.a3=16.a4=29.可知a22≠a1a3.故S2.S3中必有一个数算错了．若S2算错了.则a4=29=a1q3..显然S3=36≠8(1+q+q2).矛盾．只可能是S3算错了.此时由a2=12得.a3=18.a4=27.S4=S2+18+27=65.满足题设．
网址：http://m.1010jiajiao.com/timu3_id_531379[举报]
某同学回答“用数学归纳法证明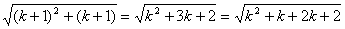
＜n+1(n∈N)”的过程如下:
＜n+1(n∈N)”的过程如下:证明：(1)当n=1时,显然命题是正确的;(2)假设n=k时有
＜k+1,那么当n=k+1时,
=(k+1)+1,所以当n=k+1时命题是正确的,由(1)(2)可知对于n∈N,命题都是正确的.以上证法是错误的,错误在于( )
A.当n=1时,验证过程不具体
B.归纳假设的写法不正确
C.从k到k+1的推理不严密
D.从k到k+1的推理过程没有使用归纳假设
查看习题详情和答案>>
某同学回答“用数学归纳法证明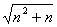
＜n+1(n∈N)”的过程如下：
＜n+1(n∈N)”的过程如下：证明：（1）当n=1时，显然命题是正确的；（2）假设n=k时有
＜k+1，那么当n=k+1时，
(k+1)+1，所以当n=k+1时命题是正确的，由（1）、（2）可知对于（n∈N）,命题都是正确的.以上证法是错误的，错误在于（ ）
A.当n=1时，验证过程不具体
B.归纳假设的写法不正确
C.从k到k+1的推理不严密
D.从k到k+1的推理过程没有使用归纳假设
查看习题详情和答案>>（2010•福建模拟）考察等式：
+
+…+
=
（*），其中n、m、r∈N*，r≤m＜n且r≤n-m．某同学用概率论方法证明等式（*）如下：
设一批产品共有n件，其中m件是次品，其余为正品．现从中随机取出r件产品，
记事件Ak={取到的r件产品中恰有k件次品}，则P(Ak)=
，k=0，1，2，…，r．
显然A0，A1，…，Ar为互斥事件，且A0∪A1∪…∪Ar=Ω（必然事件），
因此1=P（Ω）=P（A0）+P（A1）+…P（Ar）=
，
所以
+
+…+
=
，即等式（*）成立．
对此，有的同学认为上述证明是正确的，体现了偶然性与必然性的统一；但有的同学对上述证明方法的科学性与严谨性提出质疑．现有以下四个判断：
①等式（*）成立 ②等式（*）不成立 ③证明正确 ④证明不正确
试写出所有正确判断的序号
查看习题详情和答案>>
| C | 0 m |
| C | r n-m |
| C | 1 m |
| C | r-1 n-m |
| C | r m |
| C | 0 n-m |
| C | r n |
设一批产品共有n件，其中m件是次品，其余为正品．现从中随机取出r件产品，
记事件Ak={取到的r件产品中恰有k件次品}，则P(Ak)=
| ||||
|
显然A0，A1，…，Ar为互斥事件，且A0∪A1∪…∪Ar=Ω（必然事件），
因此1=P（Ω）=P（A0）+P（A1）+…P（Ar）=
| ||||||||||||
|
所以
| C | 0 m |
| C | r n-m |
| C | 1 m |
| C | r-1 n-m |
| C | r m |
| C | 0 n-m |
| C | r n |
对此，有的同学认为上述证明是正确的，体现了偶然性与必然性的统一；但有的同学对上述证明方法的科学性与严谨性提出质疑．现有以下四个判断：
①等式（*）成立 ②等式（*）不成立 ③证明正确 ④证明不正确
试写出所有正确判断的序号
①③
①③
．
，
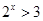”的否定是“
，
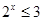”；②函数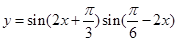
的最小正周期是
；③命题“函数
在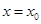
处有极值，则
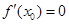”的否命题是真命题；④
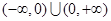上的奇函数，
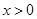的解析式是
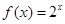，则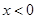
时的解析式为
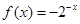．其中正确的说法是__________．
