摘要:解:由时.可得: (1)令 就得. ∴ , -----------------2分 若.则. ∴从而的当时.,---4分 且 ,即得, ∴函数在上是减函数. ----------6分 (2) 由函数是上单调函数.得. ---8分 得到数列是等差数列.即:.又 ∴.即通项公式为. --10分 (3)当...... ∴..因此数列的通项公式为 . -----------12分 可以得出数列是以为首项.以为公差的等差数列. ∴数列前项和为: . ----14分 本资料由 提供!
网址:http://m.1010jiajiao.com/timu3_id_529502[举报]
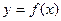 对于任意
对于任意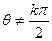 (
(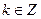 ),都有式子
),都有式子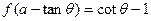 成立(其中
成立(其中 为常数).
为常数).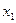 ,令
,令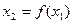 ,
,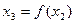 ,…,
,…,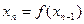 ,…
,… 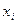 (
(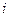 =1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果
=1,2,3,…)在定义域中,那么构造数列的过程继续下去;如果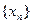 ?若存在,求出
?若存在,求出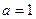 时,若
时,若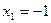 ,求数列
,求数列