摘要： 标准椭圆的两焦点为.在椭圆上.且. (1 ) 求椭圆方程. (2) 若N在椭圆上.O为原点.直线的方向向量为.若交椭圆于A.B两点.且NA.NB与轴围成的三角形是等腰三角形(两腰所在的直线是NA.NB).则称N点为椭圆的特征点.求该椭圆的特征点.
网址：http://m.1010jiajiao.com/timu3_id_529431[举报]
（本小题满分12分）标准椭圆
的两焦点为
，
在椭圆上，且
. （1）求椭圆方程；（2）若N在椭圆上，O为原点，直线
的方向向量为
，若交椭圆于A、B两点，且NA、NB与
轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB)，则称N点为椭圆的特征点，求该椭圆的特征点.
（本小题满分12分）标准椭圆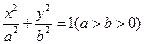
的两焦点为
，
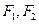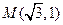在椭圆上，且
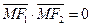. （1）求椭圆方程；（2）若N在椭圆上，O为原点，直线
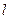的方向向量为
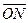，若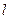交椭圆于A、B两点，且NA、NB与
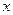轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB)，则称N点为椭圆的特征点，求该椭圆的特征点.
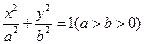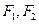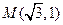的两焦点为，在椭圆上，且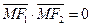. （1）求椭圆方程；（2）若N在椭圆上，O为原点，直线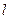的方向向量为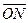，若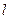交椭圆于A、B两点，且NA、NB与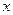轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB)，则称N点为椭圆的特征点，求该椭圆的特征点.
椭圆C的中心坐标为原点O，焦点在y轴上，焦点到相应准线的距离以及离心率均为
，直线l与y轴交于点P（0，m），与椭圆C交于相异两点A且
=λ
．
（1）求椭圆方程；
（2）若
+λ
=4
，求m的取值范围?．
查看习题详情和答案>>
| ||
| 2 |
| AP |
| PB |
（1）求椭圆方程；
（2）若
| OA |
| OB |
| OP |