摘要:方法1: (1)过S作..连 ∴ ∴ --4分 (2)..∴是平行四边形 故平面 过A作..连 ∴为平面和 二面角平面角.而 应用等面积:. ∵. 故题中二面角为 --4分 (3)∵∥.到距离为到距离 又∵..∴平面.∴平面 ∴平面平面.只需B作SE垂直BO1.BO1= 设线面角为... ∴.故线面角为 --4分 方法2: (1)同上 (2)建立直角坐标系 平面SDC法向量为. .. 设平面SAD法向量 .取.. ∴ ∴ ∴二面角为 (3)设线面角为. ∴
网址:http://m.1010jiajiao.com/timu3_id_528844[举报]
已知双曲线
-
=1 (a>0,b>0)的一条渐近线方程为
x+y=0,左、右顶点分别为A、B,右焦点为F,|BF|=1,过F作直线交此双曲线的右支于P、Q两点.
(1)求双曲线的方程;
(2)若
•
=-17,求△PBQ的面积S.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求双曲线的方程;
(2)若
| OP |
| OQ |
已知双曲线
-
=1 (a>0,b>0)的一条渐近线方程为
x+y=0,左、右顶点分别为A、B,右焦点为F,|BF|=1,过F作直线交此双曲线的右支于P、Q两点.
(1)求双曲线的方程;
(2)若
•
=-17,求△PBQ的面积S.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求双曲线的方程;
(2)若
| OP |
| OQ |
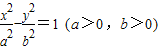 的一条渐近线方程为
的一条渐近线方程为 ,左、右顶点分别为A、B,右焦点为F,|BF|=1,过F作直线交此双曲线的右支于P、Q两点.
,左、右顶点分别为A、B,右焦点为F,|BF|=1,过F作直线交此双曲线的右支于P、Q两点.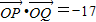 ,求△PBQ的面积S.
,求△PBQ的面积S.