摘要:在中. (Ⅰ)求, (Ⅱ)若·.求边的长. 已知函数是偶函数. (Ⅰ)求的值, (Ⅱ)若方程有解.求的取值范围. 如图.分别是三棱锥的棱的中点.过三点的平面交于. (Ⅰ)求证:四边形是平行四边形, (Ⅱ)已知..试在棱上找一点.使平面平面.并说明理由. 已知函数 (Ⅰ)若在区间上为减函数.求的取值范围, (Ⅱ)讨论在内的极值点的个数. 如图.中心在原点.焦点在轴上的椭圆的离心率.分别是椭圆的长轴.短轴的端点.原点到直线的距离为. (Ⅰ)求椭圆的标准方程, (Ⅱ)已知.设点是椭圆上的两个动点. 满足,求的取值范围. 已知数列中.当且有: . (Ⅰ)设数列满足.证明散列为等比数列.并求数列的通项公式, (Ⅱ)记.规定.求数列的前项和. 和平区2008-2009学年度第二学期高三年级
网址:http://m.1010jiajiao.com/timu3_id_528714[举报]
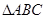 中,内角
中,内角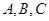 所对边的长分别为
所对边的长分别为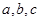 ,已知向量
,已知向量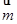 =(1,cosA -1),
=(1,cosA -1),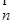 =(cosA,1)且满足
=(cosA,1)且满足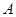 的大小;
的大小;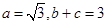 ,求
,求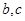 的值.
的值. 中,
中,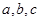 分别是角A、B、C的对边,且
分别是角A、B、C的对边,且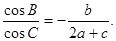
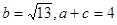 ,求
,求 中,角
中,角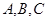 对的边分别为
对的边分别为 ,且
,且
 的值;
的值;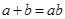 ,求
,求 。
。 中,内角
中,内角 所对边的长分别为
所对边的长分别为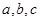 ,已知向量
,已知向量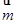 ="(1,cosA" -1),
="(1,cosA" -1),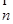 =(cosA,1)且满足
=(cosA,1)且满足 的大小;
的大小; ,求
,求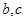 的值.
的值.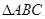 中,
中, 分别是角A、B、C的对边,且
分别是角A、B、C的对边,且
 ,求
,求