题目内容
(I)设![]() 是各项均不为零的等差数列
是各项均不为零的等差数列![]() ,且公差
,且公差![]() ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
①当![]() 时,求
时,求![]() 的数值;②求
的数值;②求![]() 的所有可能值;
的所有可能值;
(II)求证:对于一个给定的正整数![]() ,存在一个各项及公差都不为零的等差数列
,存在一个各项及公差都不为零的等差数列![]() ,其中任意三项(按原来的顺序)都不能组成等比数列。
,其中任意三项(按原来的顺序)都不能组成等比数列。
(I)①![]() ;②
;②![]()
(II)略
解析:
本小题考查等差数列与等比数列的综合运用。
(I)①当![]() 时,
时, ![]() 中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则
中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则![]() 。
。
若删去![]() ,则有
,则有![]() ,即
,即![]() ,化简得
,化简得![]() ;
;
若删去![]() ,则有
,则有![]() ,即
,即![]() ,化简得
,化简得![]() 。
。
综上可知![]() 。
。
②当![]() 时,
时, ![]() 中同样不可能删去首项或末项。
中同样不可能删去首项或末项。
若删去![]() ,则有
,则有![]() ,即
,即![]() ,化简得
,化简得![]() ;
;
若删去![]() ,则有
,则有![]() ,即
,即![]() ,化简得
,化简得![]() ,舍去;
,舍去;
若删去![]() ,则有
,则有![]() ,即
,即![]() ,化简得
,化简得![]() 。
。
当![]() 时,不存在这样的等差数列。事实上,在数列
时,不存在这样的等差数列。事实上,在数列![]() 中,由于不能删去首项和末项,若删去
中,由于不能删去首项和末项,若删去![]() ,则必有
,则必有![]() ,这与
,这与![]() 矛盾;同样若删去
矛盾;同样若删去![]() ,也有
,也有![]() ,这与
,这与![]() 矛盾;若删去
矛盾;若删去![]() 中的任意一个,则必有
中的任意一个,则必有![]() ,这与
,这与![]() 矛盾。综上可知
矛盾。综上可知![]() 。
。
(II)略

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
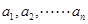 是各项均不为零的等差数列
是各项均不为零的等差数列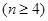 ,且公差
,且公差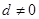 ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列: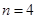 时,求
时,求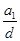 的数值;②求
的数值;②求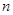 的所有可能值;
的所有可能值;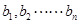 ,其中任意三项(按原来的顺序)都不能组成等比数列。
,其中任意三项(按原来的顺序)都不能组成等比数列。