摘要:1. 设数列满足其中为实数.且 (Ⅰ)求数列的通项公式 (Ⅱ)设.,求数列的前项和, (Ⅲ)若对任意成立.证明 解 (1) 方法一: 当时.是首项为.公比为的等比数列. .即 .当时.仍满足上式. 数列的通项公式为 . 方法二 由题设得:当时. 时.也满足上式. 数列的通项公式为 . 得 知 若.则 由对任意成立.知.下面证.用反证法 方法一:假设.由函数的函数图象知.当趋于无穷大时.趋于无穷大 不能对恒成立.导致矛盾.. 方法二:假设.. 即 恒成立 (*) 为常数. (*)式对不能恒成立.导致矛盾.
网址:http://m.1010jiajiao.com/timu3_id_528010[举报]
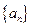 满足
满足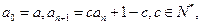 其中
其中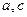 为实数,且
为实数,且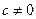
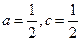 ,
,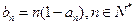 ,求数列
,求数列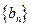 的前
的前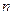 项和
项和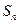 ;
;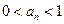 对任意
对任意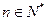 成立,证明
成立,证明