摘要:数列{an}的前n项和为Sn.且点()在函数的图象上. ⑴求数列{an} 的通项公式, ⑵设.是数列{}的前n项和.求使得对所有的都成立的最小值.
网址:http://m.1010jiajiao.com/timu3_id_527799[举报]
(本小题满分12分)已知数列{an}的前n项和为Sn, 且满足条件:4S n =![]() + 4n – 1 , nÎN*.
+ 4n – 1 , nÎN*.
(1) 证明:(a n– 2)2 –![]() =0 (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .
=0 (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .
(本小题满分12分高☆考♂资♀源?网)
已知等差数列{an}的首项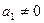 ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
(1)若a1=2,设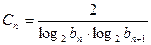 ,求数列{cn}的前n项的和Tn;
,求数列{cn}的前n项的和Tn;
(2)在(1)的条件下,若有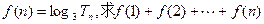 的最大值.
的最大值.
(本小题满分12分)
已知数列{an}的前n项和为Sn, Sn+1="4an+2," a1="1," bn=an+1-2an(n∈N*)
(1) 求数列{bn}的前n项和Tn.
(2)求 an
 n项和为Sn,且a3=5,S15="225."
n项和为Sn,且a3=5,S15="225."  +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn. 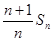
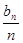 的最小值.
的最小值.