摘要：19．下表为某体育训练队跳高.跳远成绩的分布.共有队员40人.成绩分为1-5五个档次.例如表中所示跳高成绩为4分.跳远成绩为2分的队员为5人.将全部队员的姓名卡混合在一起.任取一张.该卡片队员的跳高成绩为x分.跳远成绩为y分. ⑴求m+n的值, ⑵求x=4的概率及x≥3且y=5的概率． y x 跳 远 5 4 3 2 1 跳 高 5 1 3 1 0 1 4 1 0 2 5 1 3 2 1 0 4 3 2 1 m 6 0 n 1 0 0 1 1 3
网址：http://m.1010jiajiao.com/timu3_id_527798[举报]
下表为某体育训练队跳高成绩x与跳远成绩y的分布（每名队员既跳高又跳远），成绩分别为1～5五个档次，例如表中所示跳高成绩为3分，跳远成绩为2分的队员为4人．
（I）求该训练队跳高的平均成绩；
（II）现将全部队员的姓名卡混合在一起，任取一张，该卡片队员的跳高成绩为x分，跳远成绩为y分．求y=4的概率及x+y≥8的概率． 查看习题详情和答案>>
| 跳远 | ||||||
| 5 | 4 | 3 | 2 | 1 | ||
跳高 |
5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 2 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 4 | 3 | |
| 2 | 1 | 3 | 6 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
（II）现将全部队员的姓名卡混合在一起，任取一张，该卡片队员的跳高成绩为x分，跳远成绩为y分．求y=4的概率及x+y≥8的概率． 查看习题详情和答案>>
下表为某体育训练队跳高成绩的分布，共有队员40人，成绩分为1～5五个档次，例如表中所示跳高成绩为4分，跳远成绩为2分的队员为5人．将全部队员的姓名卡混合在一起，任取一张，该卡片队员的跳高成绩为x，跳远成绩为y，设x，y为随即变量（注：没有相同姓名的队员）
（1）求x=4的概率及x≥3且y=5的概率；
（2）求m+n的值；
（3）（理）若y的数学期望为
，求m，n的值．
查看习题详情和答案>>
（1）求x=4的概率及x≥3且y=5的概率；
（2）求m+n的值；
（3）（理）若y的数学期望为
| 105 |
| 40 |
| y x |
跳 远 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
跳 高 |
5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 2 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 4 | 3 | |
| 2 | 1 | m | 6 | 0 | n | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
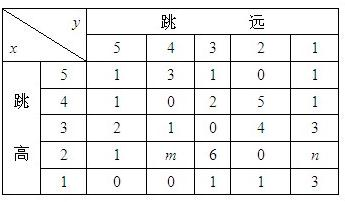下表为某体育训练队跳高与跳远成绩的统计表，全队有队员40人，成绩分为1分至5分五个档次，例如表中所示：跳高成绩为4分的人数是：1+0+2+5+1=9人；跳远成绩为2分的人数是：0+5+4+0+1=10人；跳高成绩为4分且跳远成绩为2分的队员为5人．将记载着跳高、跳远成绩的全部队员的姓名卡40张混合在一起，任取一张，记该卡片队员的跳高成绩为x，跳远成绩为y，设x，y为随机变量（注：没有相同姓名的队员）
（1）求m+n的值；
（2）求x=4的概率及x≥3且y=5的概率；
（3）若y的数学期望为
| 105 | 40 |
下表为某体育训练队跳高、跳远成绩的分布，共有队员40人，成绩分为1～5五个档次，例如表中所示跳高成绩为4分，跳远成绩为2分的队员为5人．将全部队员的姓名卡混合在一起，任取一张，该卡片队员的跳高成绩为x分，跳远成绩为y分．
（1）求m+n的值；
（2）求x=4的概率及x≥3且y=5的概率．
查看习题详情和答案>>
| y x |
跳 远 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
跳 高 |
5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 2 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 4 | 3 | |
| 2 | 1 | m | 6 | 0 | n | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
（2）求x=4的概率及x≥3且y=5的概率．
下表为某体育训练队跳高、跳远成绩的分布，共有队员40人，成绩分为1～5五个档次。例如表中所示跳高成绩为4分，跳远成绩为2分的队员为5人.将全部队员的姓名卡混合在一起，任取一张，该卡片队员的跳高成绩为x分，跳远成绩为y分.
⑴求
的值；
⑵求
的概率及
且
的概率．
|
| 跳 远 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 跳 高 | 5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 2 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 4 | 3 | |
| 2 | 1 |
| 6 | 0 |
| |
| 1 | 0 | 0 | 1 | 1 | 3 | |
