摘要：35．已知圆．以圆与坐标轴的交点分别作为双曲线的 一个焦点和顶点.则适合上述条件的双曲线的标准方程为 ． 答案:
网址：http://m.1010jiajiao.com/timu3_id_527736[举报]
已知曲线
所围成的封闭图形的面积为
，曲线
的内
切圆半径为
．记
为以曲线与坐标轴的交点为顶点的椭圆。
（I）求椭圆的标准方程，
（Ⅱ）设AB是过椭圆中心的任意弦，
是线段AB的垂直平分线。M是上异于椭圆
中心的点。
（1）若
(
为坐标原点)，当点A在椭圆上运动时，求点M的轨迹方
程；
（2）若M是与椭圆的交点，求△AMB的面积的最小值。
（2010•桂林二模）已知F1、F2是椭圆C：
+
=1（a＞b＞0）的左、右焦点，O为坐标原点，椭圆上的点到焦点距离的最大值为
+1，最小值为
-1
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知⊙O是以F1F2为直径的圆，一直线l：y=kx+m与⊙O相切，与椭圆C交于不同的两点A（x1，y1）、B（x2，y2），且满足
≤x2•x2+y1•y2≤
，求△AOB面积S的最大值．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知⊙O是以F1F2为直径的圆，一直线l：y=kx+m与⊙O相切，与椭圆C交于不同的两点A（x1，y1）、B（x2，y2），且满足
| 2 |
| 3 |
| 3 |
| 4 |
（2013•许昌三模）如图，已知C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交直线AB于点G．
与坐标轴的两个交点，且经过抛物线
的焦点，则圆C的方程为 ．
与坐标轴的两个交点，且经过抛物线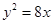
的焦点，则圆C的方程为 ．