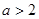摘要:15.. 已知函数(m为常数.且m>0)有极大值9. (Ⅰ)求m的值, (Ⅱ)若斜率为-5的直线是曲线的切线.求此直线方程. 解:(Ⅰ) f’(x)=3x2+2mx-m2=(x+m)(3x-m)=0,则x=-m或x=m, 当x变化时.f’(x)与f(x)的变化情况如下表: x (-∞,-m) -m (-m,) (,+∞) f’(x) + 0 - 0 + f (x) 极大值 极小值 从而可知.当x=-m时.函数f(x)取得极大值9. 即f(-m)=-m3+m3+m3+1=9,∴m=2. 知.f(x)=x3+2x2-4x+1, 依题意知f’(x)=3x2+4x-4=-5.∴x=-1或x=-. 又f(-1)=6.f(-)=. 所以切线方程为y-6=-5(x+1),或y-=-5(x+). 即5x+y-1=0.或135x+27y-23=0.
网址:http://m.1010jiajiao.com/timu3_id_527700[举报]
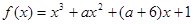 有极大值和极小值,则
有极大值和极小值,则 的取值范围为( )
的取值范围为( )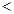
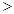 2
2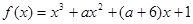 有极大值和极小值,则
有极大值和极小值,则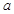 的取值范围为( )
的取值范围为( )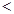
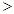 2
2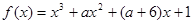 有极大值和极小值,则实数
有极大值和极小值,则实数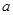 的取值范围是
的取值范围是
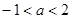 B.
B.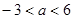 C.
C.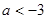 或
或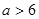 D.
D. 或
或