摘要:13.已知是实数.函数. (Ⅰ)若.求的值及曲线在点处的切线方程, (Ⅱ)求在区间上的最大值. (Ⅰ)解:. 因为. 所以. 又当时... 所以曲线在处的切线方程为. (Ⅱ)解:令.解得.. 当.即时.在上单调递增.从而 . 当.即时.在上单调递减.从而 . 当.即时.在上单调递减.在上单调递增.从而 综上所述.
网址:http://m.1010jiajiao.com/timu3_id_527698[举报]
已知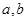 是实数,函数
是实数,函数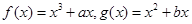 ,
,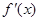 和
和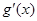 ,分别是
,分别是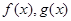 的导函数,若
的导函数,若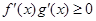 在区间
在区间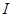 上恒成立,则称
上恒成立,则称 和
和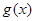 在区间
在区间 上单调性一致.
上单调性一致.
(Ⅰ)设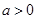 ,若函数
,若函数 和
和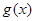 在区间
在区间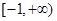 上单调性一致,求实数
上单调性一致,求实数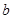 的取值范围;
的取值范围;
(Ⅱ)设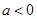 且
且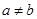 ,若函数
,若函数 和
和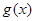 在以
在以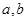 为端点的开区间上单调性一致,求
为端点的开区间上单调性一致,求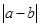 的最大值.
的最大值.
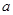 是实数,函数
是实数,函数 。
。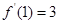 ,求
,求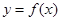 在点
在点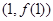 处的切线方程;
处的切线方程;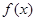 在区间
在区间 上的最大值。
上的最大值。 是实数,函数
是实数,函数 ,
, 和
和 ,分别是
,分别是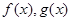 的导函数,若
的导函数,若 在区间
在区间 上恒成立,则称
上恒成立,则称 和
和 在区间
在区间 ,若函数
,若函数 上单调性一致,求实数
上单调性一致,求实数 的取值范围;
的取值范围; 且
且 ,若函数
,若函数 的最大值.
的最大值.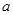 是实数,函数
是实数,函数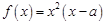 .
.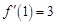 ,求
,求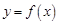 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间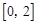 上的最大值.
上的最大值.