摘要:7. 设函数在.处取得极值.且. (Ⅰ)若.求的值.并求的单调区间, (Ⅱ)若.求的取值范围. 解:.①················································································ 2分 (Ⅰ)当时. , 由题意知为方程的两根.所以 . 由.得.··························································································· 4分 从而.. 当时.,当时.. 故在单调递减.在.单调递增.···································· 6分 (Ⅱ)由①式及题意知为方程的两根. 所以. 从而. 由上式及题设知.························································································· 8分 考虑. .········································································ 10分 故在单调递增.在单调递减.从而在的极大值为. 又在上只有一个极值.所以为在上的最大值.且最小值为. 所以.即的取值范围为.··············································· 14分
网址:http://m.1010jiajiao.com/timu3_id_527692[举报]
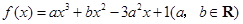 在
在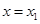 ,
,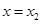 处取得极值,且
处取得极值,且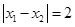 .
.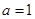 ,求
,求 的值,并求
的值,并求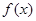 的单调区间;
的单调区间;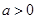 ,求
,求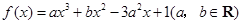 在
在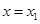 ,
,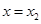 处取得极值,且
处取得极值,且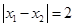 .
.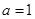 ,求
,求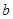 的值,并求
的值,并求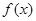 的单调区间;
的单调区间;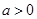 ,求
,求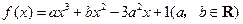 在
在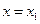 ,
,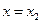 处取得极值,且
处取得极值,且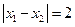 .
.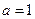 ,求
,求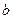 的值,并求
的值,并求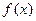 的单调区间;
的单调区间;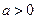 ,求
,求