摘要:14.甲.乙两名围棋选手在一次比赛中对局.分析甲胜的概率比乙胜的概率高5%.和棋的概率为59%.则乙胜的概率为 .
网址:http://m.1010jiajiao.com/timu3_id_527480[举报]
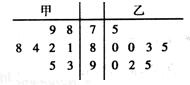 上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图:
上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图:(1)现在从甲、乙两人中选一人担任客流高峰阶段的安检员,从统计学的角度考虑,你认为选派哪位安检员参加合适?请说明理由;
(2)若将频率视为概率,甲安检员在正式开园的一个工作日的4小时内,每个单位小时段安检人数高于80人的次数记为ξ,求ξ的分布列及数学期望Eξ. 查看习题详情和答案>>
甲、乙两名射手各进行一次射击,射中环数ξ1,ξ2的分布列分别为:
(I)确定a、b的值,并求两人各进行一次射击,都射中10环的概率;
(II)两各射手各射击一次为一轮射击,如果在某一轮射击中两人都射中10环,则射击结束,否则继续射击,但最多不超过4轮,求结束时射击轮次数η的分布列及期望,并求结束时射击轮次超过2次的概率.
查看习题详情和答案>>
| ξ1 | 8 | 9 | 10 |
| P | 0.3 | 0.5 | a |
| ξ2 | 8 | 9 | 10 |
| P | 0.2 | 0.3 | b |
(II)两各射手各射击一次为一轮射击,如果在某一轮射击中两人都射中10环,则射击结束,否则继续射击,但最多不超过4轮,求结束时射击轮次数η的分布列及期望,并求结束时射击轮次超过2次的概率.
甲、乙两名跳高运动员,一次试跳2米高度成功的概率分别为0.7、0.6,假如每次试跳成功与否之间没有没有影响.求:
(1)甲试跳三次,第三次才成功的概率;
(2)甲、乙两人在第一次试跳中至少有一人成功的概率.
查看习题详情和答案>>
(1)甲试跳三次,第三次才成功的概率;
(2)甲、乙两人在第一次试跳中至少有一人成功的概率.
甲、乙两名射击运动员在某次测试中各射击20次,两人的测试成绩如表
s1,s2分别表示甲乙两名运动员在这次测试中成绩的标准差,
,
分别表示甲、乙两名运动员这次测试中成绩的平均数,则有( )
| 甲的成绩 | 乙的成绩 | |||||||||
| 环数 | 7 | 8 | 9 | 10 | 环数 | 7 | 8 | 9 | 10 | |
| 频数 | 6 | 4 | 4 | 6 | 频数 | 4 | 6 | 6 | 4 | |
. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
甲、乙两名射击运动员在某次测试中各射击20次,两人的测试成绩如下表
|
甲的成绩 |
|
乙的成绩 |
||||||||
|
环数 |
7 |
8 |
9 |
10 |
|
环数 |
7 |
8 |
9 |
10 |
|
频数 |
6 |
4 |
4 |
6 |
|
频数 |
4 |
6 |
6 |
4 |
s1,s2分别表示甲乙两名运动员在这次测试中成绩的标准差,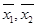 分别表示甲、乙两名运
分别表示甲、乙两名运
动员这次测试中成绩的平均数,则有
A.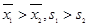 B.
B.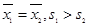 C.
C.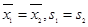 D.
D.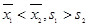
查看习题详情和答案>>