题目内容
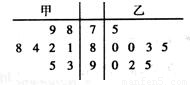
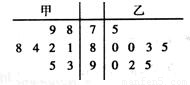
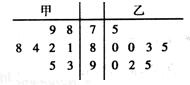 上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图:
上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图:(1)现在从甲、乙两人中选一人担任客流高峰阶段的安检员,从统计学的角度考虑,你认为选派哪位安检员参加合适?请说明理由;
(2)若将频率视为概率,甲安检员在正式开园的一个工作日的4小时内,每个单位小时段安检人数高于80人的次数记为ξ,求ξ的分布列及数学期望Eξ.
分析:(1)由茎叶图可以看出甲和乙的成绩,算出甲的平均数和乙的平均数,两个人的平均数是相同的,不好比较,再求出两个人的方差,甲的方差小于乙的方差,得到甲的成绩比较稳定,可以派甲去.
(2)由题意知每个单位小时段安检人数高于80人的次数记为ξ,随机变量ξ的可能取值为0、1、2、3,从所给的条件可以看出ξ~B(4,
).这样代入公式,可以求出变量对应的事件的概率,写出分布列和期望.
(2)由题意知每个单位小时段安检人数高于80人的次数记为ξ,随机变量ξ的可能取值为0、1、2、3,从所给的条件可以看出ξ~B(4,
| 3 |
| 4 |
解答:解:(1)派甲参赛比较合适.
理由如下:
甲=
(70×2+80×4+90×2+8+9+1+2+4+8+3+5)=85,
乙=
(70×1+80×4+90×3+5+0+0+3+5+0+2+5)=85,
=
[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2
+(90-85)2+(92-85)2+(95-85)2]=35.5
S乙2=
[(75-85)2+(80-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41
∵
甲=
乙,
<
,
∴甲的成绩较稳定,派甲参赛比较合适.
(2)记“甲安检员在一小时内完成安检人数高于80人”为事件A,P(A)=
=
.
每个单位小时段安检人数高于80人的次数记为ξ,
随机变量ξ的可能取值为0、1、2、3,且ξ~B(4,
).
∴P(ξ=k)=
(
)k(
)4-k(k=0,1,2,3,4)
∴变量ξ的分布列为:
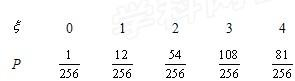
∴Eξ=4×
=3
理由如下:
. |
| x |
| 1 |
| 8 |
. |
| x |
| 1 |
| 8 |
| s | 2 甲 |
| 1 |
| 8 |
+(90-85)2+(92-85)2+(95-85)2]=35.5
S乙2=
| 1 |
| 8 |
∵
. |
| x |
. |
| x |
| s | 2 甲 |
| s | 2 乙 |
∴甲的成绩较稳定,派甲参赛比较合适.
(2)记“甲安检员在一小时内完成安检人数高于80人”为事件A,P(A)=
| 6 |
| 8 |
| 3 |
| 4 |
每个单位小时段安检人数高于80人的次数记为ξ,
随机变量ξ的可能取值为0、1、2、3,且ξ~B(4,
| 3 |
| 4 |
∴P(ξ=k)=
| C | k 4 |
| 3 |
| 4 |
| 1 |
| 4 |
∴变量ξ的分布列为:
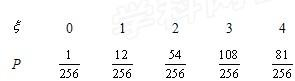
∴Eξ=4×
| 3 |
| 4 |
点评:本题考查茎叶图,平均数和方差,考查离散型随机变量的分布列和期望,是一个综合题,也是近几年高考题目中经常出现的一个问题,注意解题的格式.

练习册系列答案
相关题目
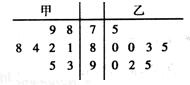 上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图:
上海世博会在游客入园参观的试运营阶段,为了解每个入口的通行速度,在一号入口处随机抽取甲、乙两名安检人员在一小时内完成游客入园人数的8次记录,记录人数的茎叶图如图: