摘要： 三角形重心坐标公式.
网址：http://m.1010jiajiao.com/timu3_id_527257[举报]
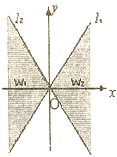如图，直线ll：y=2x与直线l2：y=-2x之间的阴影区域（不含边界）记为w，其左半部分记为w1，右半部分记为W2．（1）分别用不等式组表示w1和w2：
（2）若区域W中的动点P（x，y）到l1，l2的距离之积等于4，求点P的轨迹C的方程；
（3）设不过原点的直线l与曲线C相交于Ml，M2两点，且与ll，l2如分别交于M3，M4两点．求证△OMlM2的重心与△OM3M4的重心重合．
【三角形重心坐标公式：△ABC的顶点坐标为A（xl，y1），B（x2，y2），C（x3，y3），则△ABC的重心坐标为（
| x1+x2+x3 |
| 3 |
| y1+y2+y3 |
| 3 |
(1)定比分点公式:设点P分
所成的比为λ,即
=λ(λ≠-1)且A(x1,y1),B(x2,y2),P(x,y),则x= ,y= .?
所成的比为λ,即 =λ(λ≠-1)且A(x1,y1),B(x2,y2),P(x,y),则x= ,y= .? (2)对λ的讨论:?
①点P在
上(但不与B重合)时,λ .特别地,当λ=0时,P与A ；λ=1时,P是
的 ,得 坐标公式:x= , y= .?
②点P在
的延长线上时,λ .?
③点P在
的延长线(即
的反向延长线)上时, .?
(3)三角形重心坐标公式:△ABC中,A(x1,y1),B(x2,y2),C(x3,y3),重心G(x,y),则有x= ,y= .
查看习题详情和答案>>
如图，直线ll：y=2x与直线l2：y=-2x之间的阴影区域（不含边界）记为w，其左半部分记为w1，右半部分记为W2．
（1）分别用不等式组表示w1和w2：
（2）若区域W中的动点P（x，y）到l1，l2的距离之积等于4，求点P的轨迹C的方程；
（3）设不过原点的直线l与曲线C相交于Ml，M2两点，且与ll，l2如分别交于M3，M4两点．求证△OMlM2的重心与△OM3M4的重心重合．
【三角形重心坐标公式：△ABC的顶点坐标为A（xl，y1），B（x2，y2），C（x3，y3），则△ABC的重心坐标为（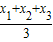
，
）】
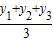查看习题详情和答案>>
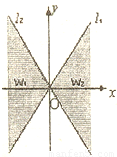
（1）分别用不等式组表示w1和w2：
（2）若区域W中的动点P（x，y）到l1，l2的距离之积等于4，求点P的轨迹C的方程；
（3）设不过原点的直线l与曲线C相交于Ml，M2两点，且与ll，l2如分别交于M3，M4两点．求证△OMlM2的重心与△OM3M4的重心重合．
【三角形重心坐标公式：△ABC的顶点坐标为A（xl，y1），B（x2，y2），C（x3，y3），则△ABC的重心坐标为（
，）】
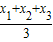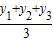查看习题详情和答案>>
如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．