摘要：设函数f (x)的定义域为R.对任意实数α.β.有f (α)+f (β)=2f ·f,且 ,. (1)求f (0)及的值. (2)求证:f (-x)=f (x)=-f (π-x). (3)若0≤x<时.f (x)>0.求证:f (x)在［0,π］上单调递减.
网址：http://m.1010jiajiao.com/timu3_id_526934[举报]
设函数f(x)的定义域为R，对任意数a、b有f(a)+f(b)=
,且
（1）求证：f(-x)=f(x)=-f(p-x)
（2）若0£x£
时，f(x)>0，求证：f(x)在[0，p]上单调递减；
（3）求f(x)的最小周期并加以证明．
查看习题详情和答案>>
设函数f(x)的定义域为R，对任意数a、b有f(a)+f(b)=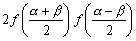
,且
,且
（1）求证：f(-x)=f(x)=-f(p-x)
（2）若0£x£
时，f(x)>0，求证：f(x)在[0，p]上单调递减；
（3）求f(x)的最小周期并加以证明．
查看习题详情和答案>>设函数f(x)的定义域为R，对任意实数x、y都有f(x＋y)＝f(x)＋f(y)，当x＞0时f(x)＜0，且f(3)＝－4．
(1)求f(0)，f(1)的值
(2)求证：f(x)为奇函数；
(3)在区间[－9，9]上，求f(x)的最值．
，试解不等式：
(
且
)