摘要:3. 解:(I) ∵x>0.∴ ∴f上为减函数.在上是增函数. 由0<a<b.且f. 可得 0<a1<b和. 即. ∴2ab=a+b>. 故.即ab>1. (II)不存在满足条件的实数a.b. 若存在满足条件的实数a.b.使得函数y=的定义域.值域都是 [a.b].则a>0. ① 当时.在(0.1)上为减函数. 故 即 解得 a=b. 故此时不存在适合条件的实数a.b. ② 当时.在上是增函数. 故 即 此时a.b是方程的根.此方程无实根. 故此时不存在适合条件的实数a.b. ③ 当.时. 由于.而. 故此时不存在适合条件的实数a.b. 综上可知.不存在适合条件的实数a.b. (III)若存在实数a.b.使得函数y=f(x)的定义域为[a.b]时.值域为[ma.mb]. 则a>0.m>0. ① 当时.由于f上是减函数.故.此时刻得a,b异号.不符合题意.所以a.b不存在. ② 当或时.由(II)知0在值域内.值域不可能是[ma.mb].所以a.b不存在. 故只有. ∵在上是增函数. ∴ 即 a. b是方程的两个根. 即关于x的方程有两个大于1的实根. 设这两个根为.. 则+=.·=. ∴ 即 解得 . 故m的取值范围是.
网址:http://m.1010jiajiao.com/timu3_id_526846[举报]
已知函数f(x)=(ax2+x)ex,其中e是自然数的底数,a∈R.
(1)当a<0时,解不等式f(x)>0;
(2)若f(x)在[-1,1]上是单调函数,求a的取值范围;
(3)当a=0时,求整数k的所有值,使方程f(x)=x+2在[k,k+1]上有解.
设函数f(x)=lnx,g(x)=ax+ ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
(Ⅰ)求a、b的值;
(Ⅱ)设x>0,试比较f(x)与g(x)的大小.[来源:学,科,网Z,X,X,K]
【解析】第一问解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
第二问,由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
(11)由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
查看习题详情和答案>>
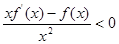 成立,则不等式
成立,则不等式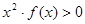 的解集是( )
的解集是( )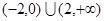 B.
B.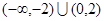
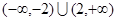 D.
D.