摘要:19. 定义在D上的函数.如果满足:.常数.都有≤M成立.则称是D上的有界函数.其中M称为函数的上界. (Ⅰ)试判断函数在[1.3]上是不是有界函数?请给出证明, (Ⅱ)若已知质点的运动方程为.要使在上的每一时刻的瞬时速度是以M=1为上界的有界函数.求实数a的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_526372[举报]
(本小题满分14分)定义在D上的函数![]() ,如果满足;对任意
,如果满足;对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数![]() 的上界。已知函数
的上界。已知函数![]() ,
,![]() 当
当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;若函数
上是否为有界函数,请说明理由;若函数![]() 在
在![]() 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数![]() 的取值范围;若
的取值范围;若![]() ,求函数
,求函数![]() 在
在![]() 上的上界T的取值范围。
上的上界T的取值范围。
(本小题满分14分)对于定义在区间D上的函数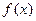 ,若存在闭区间
,若存在闭区间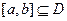 和常数
和常数 ,使得对任意
,使得对任意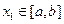 ,都有
,都有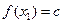 ,且对任意
,且对任意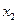 ∈D,当
∈D,当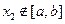 时,
时,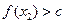 恒成立,则称函数
恒成立,则称函数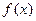 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数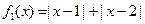 和
和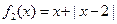 是否为R上的“平底
是否为R上的“平底 型”函数? 并说明理由;
型”函数? 并说明理由;
(Ⅱ)设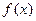 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式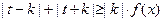 对一切
对一切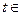 R恒成立,求实数
R恒成立,求实数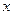 的取值范围;
的取值范围;
(Ⅲ)若函数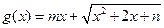 是区间
是区间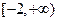 上的“平底型”函数,求
上的“平底型”函数,求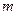 和
和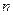 的值.
的值.
.
(本小题满分14分)
已知函数
(Ⅰ)请研究函数 的单调性;
的单调性;
(Ⅱ)若函数 有两个零点,求实数
有两个零点,求实数 的取值范围;
的取值范围;
(Ⅲ)若定义在区间D上的函数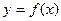 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式 成立,则称函数
成立,则称函数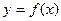 为区间D上的“凹函数”.若函
为区间D上的“凹函数”.若函
数 的最小值为
的最小值为 ,试判断函数
,试判断函数 是否为“凹函数”,并对你的判断加以证明.
是否为“凹函数”,并对你的判断加以证明.
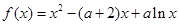 ,其中常数
,其中常数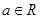 .
.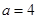 时,求函数
时,求函数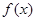 的极值点;
的极值点; ,若函数
,若函数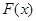 在区间
在区间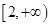 上单调递增,求
上单调递增,求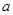 的取值范围;
的取值范围;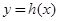 在点
在点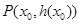 处的切线方程为
处的切线方程为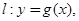 当
当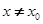 时,若
时,若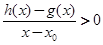 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数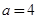 时,函数
时,函数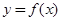 是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.
是否存在“特殊点”,若存在,请最少求出一个“特殊点”的横坐标,若不存在,说明理由.
 的单调性;
的单调性;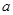 的取值范围;
的取值范围;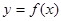 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式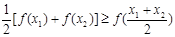 成立,则称函数
成立,则称函数 ,试判断函数
,试判断函数