摘要：8．若圆.上至少有三个不同的点到直线的距离为.则直线z的倾斜角的取值范围是 A． B． C． D．
网址：http://m.1010jiajiao.com/timu3_id_525430[举报]
已知以点C （t，
）（t∈R），t≠0）为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为坐标原点．
（1）求证：△OAB的面积为定值．
（2）设直线y=-2x+4与圆C交于点M，N若|OM|=|ON|，求圆C的方程．
（3）若t＞0，当圆C的半径最小且时，圆C上至少有三个不同的点到直线l：y-
=k(x-3-
)的距离为
，求直线l的斜率k的取值范围．
查看习题详情和答案>>
| 2 |
| t |
（1）求证：△OAB的面积为定值．
（2）设直线y=-2x+4与圆C交于点M，N若|OM|=|ON|，求圆C的方程．
（3）若t＞0，当圆C的半径最小且时，圆C上至少有三个不同的点到直线l：y-
| 2 |
| 2 |
| 1 |
| 2 |
已知以点C (t,
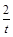)（t∈R），t≠0）为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为坐标原点．
（1）求证：△OAB的面积为定值；
（2）设直线y= –2x+4与圆C交于点M，N若|OM|=|ON|，求圆C的方程．
（3）若t＞0，当圆C的半径最小时，圆C上至少有三个不同的点到直线l：y –
的距离为
，求直线l的斜率k的取值范围．
查看习题详情和答案>>
已知以点C （t，
）（t∈R），t≠0）为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为坐标原点．
（1）求证：△OAB的面积为定值．
（2）设直线y=-2x+4与圆C交于点M，N若|OM|=|ON|，求圆C的方程．
（3）若t＞0，当圆C的半径最小且时，圆C上至少有三个不同的点到直线l：y-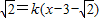
的距离为
，求直线l的斜率k的取值范围．
查看习题详情和答案>>
）（t∈R），t≠0）为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为坐标原点．（1）求证：△OAB的面积为定值．
（2）设直线y=-2x+4与圆C交于点M，N若|OM|=|ON|，求圆C的方程．
（3）若t＞0，当圆C的半径最小且时，圆C上至少有三个不同的点到直线l：y-
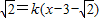的距离为，求直线l的斜率k的取值范围．查看习题详情和答案>>
已知以点C(t，
)(t∈R)，t≠0)为圆心的圆与x轴交于点O，A，与y轴交于点O，B，其中O为坐标原点．
(1)求证：△OAB的面积为定值；
(2)设直线y＝－2x＋4与圆C交于点M，N若|OM|＝|ON|，求圆C的方程．
(3)若t＞0，当圆C的半径最小时，圆C上至少有三个不同的点到直线l：y－
＝k(x－3－
)的距离为
，求直线l的斜率k的取值范围．
若圆x2+y2-4x-4y-10=0上至少有三个不同的点到直线l：ax+by=0的距离为2
，则直线l的倾斜角的取值范围是（ ）
| 2 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[0，
|